
【題目】已知橢圓![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() ,
, ![]() ,點
,點 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)是否存在斜率為2的直線![]() ,使得當(dāng)直線
,使得當(dāng)直線![]() 與橢圓
與橢圓![]() 有兩個不同交點
有兩個不同交點![]() 時,能在直線
時,能在直線![]() 上找到一點
上找到一點![]() ,在橢圓
,在橢圓![]() 上找到一點
上找到一點![]() ,滿足
,滿足![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
【答案】(1)![]() ;(2)不存在,理由見解析.
;(2)不存在,理由見解析.
【解析】試題分析:(1)由焦點坐標(biāo)可得![]() ,再根據(jù)
,再根據(jù)![]() 及點
及點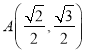 在橢圓
在橢圓![]() 上,可得
上,可得![]() ,進(jìn)而可得橢圓的方程;(2)設(shè)直線
,進(jìn)而可得橢圓的方程;(2)設(shè)直線![]() 的方程為
的方程為![]() ,與橢圓方程聯(lián)立可得
,與橢圓方程聯(lián)立可得![]() ,與判別式為正可得
,與判別式為正可得![]() ,再根據(jù)平行四邊形性質(zhì)及韋達(dá)定理可得點
,再根據(jù)平行四邊形性質(zhì)及韋達(dá)定理可得點![]() 的縱坐標(biāo)范圍是
的縱坐標(biāo)范圍是![]() ,可判定點
,可判定點![]() 不在橢圓上,所以這樣的直線
不在橢圓上,所以這樣的直線![]() 不存在.
不存在.
試題解析:(1)設(shè)橢圓![]() 的焦距為
的焦距為![]() ,則
,則![]() ,
,
因此橢圓方程為![]()
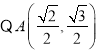 在橢圓上,
在橢圓上, 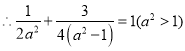 解得
解得![]()
故橢圓![]() 的方程為
的方程為![]() .
.
(2)假設(shè)存在這樣的直線 設(shè)直線![]() 的方程為
的方程為![]() ,
,
設(shè)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中點為
的中點為![]() ,
,
由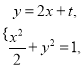 得
得![]() ,
,
所以![]() ,且
,且![]() ,則
,則![]() ,
,
![]()
![]()
由![]() 知四邊形
知四邊形![]() 為平行四邊形,
為平行四邊形,
而![]() 為線段
為線段![]() 的中點,因此,
的中點,因此, ![]() 也是線段
也是線段![]() 的中點,
的中點,
所以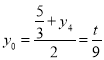 ,可得
,可得![]() ,
,
又![]() ,所以
,所以![]() ,
,
因此點![]() 不在橢圓上.
不在橢圓上.
所以這樣的直線l不存在
【方法點晴】本題主要考查待定系數(shù)法求橢圓的標(biāo)準(zhǔn)方程、韋達(dá)定理以及解析幾何中的存在性問題,屬于難題.解決存在性問題,先假設(shè)存在,推證滿足條件的結(jié)論,若結(jié)論正確則存在,若結(jié)論不正確則不存在,注意:①當(dāng)條件和結(jié)論不唯一時要分類討論;②當(dāng)給出結(jié)論而要推導(dǎo)出存在的條件時,先假設(shè)成立,再推出條件;③當(dāng)條件和結(jié)論都不知,按常規(guī)方法題很難時采取另外的途徑.


 奪冠訓(xùn)練單元期末沖刺100分系列答案
奪冠訓(xùn)練單元期末沖刺100分系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高一學(xué)生共有500人,為了了解學(xué)生的歷史學(xué)習(xí)情況,隨機(jī)抽取了50名學(xué)生,對他們一年來4次考試的歷史平均成績進(jìn)行統(tǒng)計,得到頻率分布直方圖如圖所示,后三組頻數(shù)成等比數(shù)列.
(1)求第五、六組的頻數(shù),補全頻率分布直方圖;
(2)若每組數(shù)據(jù)用該組區(qū)間中點值(例如區(qū)間[70,80)的中點值是
75作為代表,試估計該校高一學(xué)生歷史成績的平均分;
(3)估計該校高一學(xué)生歷史成績在70~100分范圍內(nèi)的人數(shù).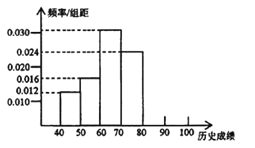
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 為參數(shù)
為參數(shù)![]() 和直線
和直線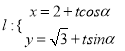
![]() 其中
其中![]() 為參數(shù),
為參數(shù), ![]() 為直線
為直線![]() 的傾斜角
的傾斜角![]() .
.
(1)當(dāng)![]() 時,求圓上的點到直線
時,求圓上的點到直線![]() 的距離的最小值;
的距離的最小值;
(2)當(dāng)直線![]() 與圓
與圓![]() 有公共點時,求
有公共點時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐V﹣ABCD中,底面ABCD是正方形,側(cè)棱VA⊥底面ABCD,點E為VA的中點.
(Ⅰ)求證:VC∥平面BED;
(Ⅱ)求證:平面VAC⊥平面BED.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l過點P(0,2),斜率為k,圓Q:x2+y2﹣12x+32=0.
(1)若直線l和圓相切,求直線l的方程;
(2)若直線l和圓交于A、B兩個不同的點,問是否存在常數(shù)k,使得![]() +
+![]() 與
與![]() 共線?若存在,求出k的值;若不存在,請說明理由.
共線?若存在,求出k的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于圓周率![]() ,數(shù)學(xué)發(fā)展史上出現(xiàn)過許多很有創(chuàng)意的求法,如著名的蒲豐實驗和查理斯實驗.受其啟發(fā),我們也可以通過設(shè)計下面的實驗來估計
,數(shù)學(xué)發(fā)展史上出現(xiàn)過許多很有創(chuàng)意的求法,如著名的蒲豐實驗和查理斯實驗.受其啟發(fā),我們也可以通過設(shè)計下面的實驗來估計![]() 的值:先請200名同學(xué),每人隨機(jī)寫下一個都小于1的正實數(shù)對(x,y);再統(tǒng)計兩數(shù)能與1構(gòu)成鈍角三角形三邊的數(shù)對(x,y)的個數(shù)m;最后再根據(jù)統(tǒng)計數(shù)m來估計
的值:先請200名同學(xué),每人隨機(jī)寫下一個都小于1的正實數(shù)對(x,y);再統(tǒng)計兩數(shù)能與1構(gòu)成鈍角三角形三邊的數(shù)對(x,y)的個數(shù)m;最后再根據(jù)統(tǒng)計數(shù)m來估計![]() 的值.假如統(tǒng)計結(jié)果是m=56,那么可以估計
的值.假如統(tǒng)計結(jié)果是m=56,那么可以估計![]() __________.(用分?jǐn)?shù)表示)
__________.(用分?jǐn)?shù)表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知中心在原點,焦點在![]() 軸上的橢圓
軸上的橢圓![]() 過點
過點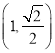 ,離心率為
,離心率為![]() ,
, ![]() ,
, ![]() 是橢圓
是橢圓![]() 的長軸的兩個端點(
的長軸的兩個端點(![]() 位于
位于![]() 右側(cè)),
右側(cè)),![]() 是橢圓在
是橢圓在![]() 軸正半軸上的頂點.
軸正半軸上的頂點.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)是否存在經(jīng)過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 和
和![]() ,使得向量
,使得向量![]() 與
與![]() 共線?如果存在,求出直線方程;如果不存在,請說明理由.
共線?如果存在,求出直線方程;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】命題p:函數(shù)y=log2(x2﹣2x)的單調(diào)增區(qū)間是[1,+∞),命題q:函數(shù)y=![]() 的值域為(0,1),下列命題是真命題的為( )
的值域為(0,1),下列命題是真命題的為( )
A.p∧q
B.p∨q
C.p∧(¬q)
D.¬q
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com