
【題目】(1)已知橢圓兩個焦點的坐標(biāo)分別是(-2,0),(2,0),并且經(jīng)過點![]() ,求它的標(biāo)準(zhǔn)方程;
,求它的標(biāo)準(zhǔn)方程;
(2)已知雙曲線兩個焦點的坐標(biāo)分別是(0,-6),(0,6),并且經(jīng)過點(2,-5),求它的標(biāo)準(zhǔn)方程.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由題意可設(shè)橢圓方程為![]() ,且
,且![]() ,利用橢圓定義及兩點間的距離公式求得
,利用橢圓定義及兩點間的距離公式求得![]() ,結(jié)合隱含條件求得
,結(jié)合隱含條件求得![]() ,則橢圓方程可求;
,則橢圓方程可求;
(2)由題意可設(shè)雙曲線的方程為![]() ,且
,且![]() ,利用雙曲線的定義及兩點間的距離公式求得
,利用雙曲線的定義及兩點間的距離公式求得![]() ,結(jié)合隱含條件求得
,結(jié)合隱含條件求得![]() ,則雙曲線方程可求.
,則雙曲線方程可求.
![]() 因為橢圓的焦點在
因為橢圓的焦點在![]() 軸上,所以設(shè)它的標(biāo)準(zhǔn)方程為
軸上,所以設(shè)它的標(biāo)準(zhǔn)方程為
![]()
有橢圓的定義知
![]()
![]() ,
,
![]()
又因為![]() ,所以
,所以![]()
因此,所求橢圓的標(biāo)準(zhǔn)方程為![]() .
.
(2)因為雙曲線的焦點在![]() 軸上,所以設(shè)它的標(biāo)準(zhǔn)方程為
軸上,所以設(shè)它的標(biāo)準(zhǔn)方程為
![]()
有雙曲線的定義知
![]() ,
,![]()
又因為![]() ,所以
,所以![]()
因此,所求雙曲線的標(biāo)準(zhǔn)方程為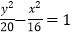 .
.


 新思維假期作業(yè)暑假吉林大學(xué)出版社系列答案
新思維假期作業(yè)暑假吉林大學(xué)出版社系列答案 藍天教育暑假優(yōu)化學(xué)習(xí)系列答案
藍天教育暑假優(yōu)化學(xué)習(xí)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)高考實行新方案,規(guī)定:語文、數(shù)學(xué)和英語是考生的必考科目,考生還須從物理,化學(xué),生物,歷史,地理和政治六個科目中選取三個科目作為選考科目.若一個學(xué)生從六個科目中選出了三個科目作為選考科目,則稱該學(xué)生的選考方案確定;否則,稱該學(xué)生選考方案待確定.例如,學(xué)生甲選擇“物理、化學(xué)和生物”三個選考科目,則學(xué)生甲的選考方案確定,“物理、化學(xué)和生物”為其選考方案.
某學(xué)校為了解高一年級420名學(xué)生選考科目的意向,隨機選取30名學(xué)生進行了一次調(diào)查,統(tǒng)計選考科目人數(shù)如下表:
性別 | 選考方案確定情況 | 物理 | 化學(xué) | 生物 | 歷史 | 地理 | 政治 |
男生 | 選考方案確定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
選考方案待確定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 選考方案確定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
選考方案待確定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估計該學(xué)校高一年級選考方案確定的學(xué)生中選考生物的學(xué)生有多少人?
(Ⅱ)假設(shè)男生、女生選擇選考科目是相互獨立的.從選考方案確定的8位男生中隨機選出1人,從選考方案確定的10位女生中隨機選出1人,試求該男生和該女生的選考方案中都含有歷史學(xué)科的概率;
(Ⅲ)從選考方案確定的8名男生中隨機選出2名,設(shè)隨機變量![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() ,
, ![]() 的中點.
的中點.
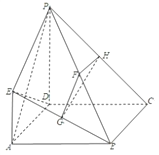
(1)求證: ![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的大小;
所成銳二面角的大小;
(3)在線段![]() 上是否存在一點
上是否存在一點![]() ,使直線
,使直線![]() 與直線
與直線![]() 所成的角為
所成的角為![]() ?若存在,求出線段
?若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出集合![]()
(1)若![]() 求證:函數(shù)
求證:函數(shù)![]()
(2)由(1)可知,![]() 是周期函數(shù)且是奇函數(shù),于是張三同學(xué)得出兩個命題:
是周期函數(shù)且是奇函數(shù),于是張三同學(xué)得出兩個命題:
命題甲:集合M中的元素都是周期函數(shù);命題乙:集合M中的元素都是奇函數(shù),請對此給出判斷,如果正確,請證明;如果不正確,請舉出反例;
(3)設(shè)![]() 為常數(shù),且
為常數(shù),且![]() 求
求![]() 的充要條件并給出證明.
的充要條件并給出證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某學(xué)校擬建一塊五邊形區(qū)域的“讀書角”,三角形區(qū)域ABE為書籍?dāng)[放區(qū),沿著AB、AE處擺放折線形書架(書架寬度不計),四邊形區(qū)域為BCDE為閱讀區(qū),若∠BAE=60°,∠BCD=∠CDE=120°,DE=3BC=3CD=![]() m.
m.
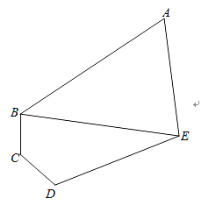
(1)求兩區(qū)域邊界BE的長度;
(2)若區(qū)域ABE為銳角三角形,求書架總長度AB+AE的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某車間為了規(guī)定工時定額,需要確定加工零件所花費的時間,為此作了四次試驗,得到的數(shù)據(jù)如下:
零件的個數(shù) |
|
|
|
|
加工的時間 |
|
|
|
|
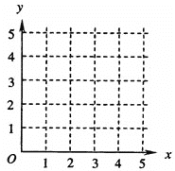
(1)在給定的坐標(biāo)系中畫出表中數(shù)據(jù)的散點圖;
(2)求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() .
.
(3)試預(yù)測加工![]() 個零件需要多少時間?
個零件需要多少時間?
附錄:參考公式: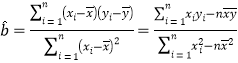 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為25cm的正方形中挖去邊長為23cm的兩個等腰直角三角形,現(xiàn)有均勻的粒子散落在正方形中,問粒子落在中間帶形區(qū)域的概率是多少?

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
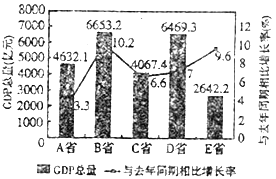
【題目】如圖是2017年第一季度中國某五省![]() 情況圖,則下列陳述正確的是( )
情況圖,則下列陳述正確的是( )
①2017年第一季度 ![]() 總量高于4000億元的省份共有3個;
總量高于4000億元的省份共有3個;
②與去年同期相比,2017年第一季度五個省的![]() 總量均實現(xiàn)了增長;
總量均實現(xiàn)了增長;
③去年同期的![]() 總量前三位依次是
總量前三位依次是![]() 省、
省、![]() 省、
省、![]() 省;
省;
④2016年同期![]() 省的
省的![]() 總量居于第四位.
總量居于第四位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在等腰![]() 中,
中, ![]() ,腰長為
,腰長為![]() ,
, ![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 的中點,將
的中點,將![]() 沿
沿![]() 翻折,得到四棱錐
翻折,得到四棱錐![]() ,且
,且![]() 為棱
為棱![]() 中點,
中點, ![]() .
.
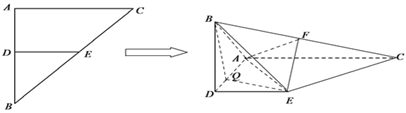
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求二面角
?若存在,求二面角![]() 的余弦值,若不存在,請說明理由.
的余弦值,若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com