
【題目】已知向量![]() ,
,![]() ,函數
,函數![]() 滿足
滿足![]() ,且在區間
,且在區間![]() 上單調,又不等式
上單調,又不等式![]() 對一切
對一切![]() 恒成立.
恒成立.
(1)求函數![]() 的解析式;
的解析式;
(2)若函數![]() 在區間
在區間![]() 的零點為
的零點為![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根據![]() 利用向量數量積公式與正弦的和角公式化簡,再根據題意可得
利用向量數量積公式與正弦的和角公式化簡,再根據題意可得![]() 的對稱軸與對稱中心等.同時利用
的對稱軸與對稱中心等.同時利用![]() 在區間
在區間![]() 上單調求出關于周期的不等式,繼而求得解析式.
上單調求出關于周期的不等式,繼而求得解析式.
(2)將題意轉換為函數![]() 的圖象與
的圖象與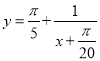 的圖象在區間
的圖象在區間![]() 上有100個交點.再利用函數的對稱點分析求解即可.
上有100個交點.再利用函數的對稱點分析求解即可.
(1)![]()
因為![]() ,所以
,所以![]() 是函數
是函數![]() 的一個對稱中心,
的一個對稱中心,
由![]() ,得
,得![]() 為函數
為函數![]() 的一條對稱軸,
的一條對稱軸,
所以![]() ,即
,即![]()
所以![]() .
.
又因為函數![]() 在區間
在區間![]() 上單調,所以
上單調,所以![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() .
.
又因為![]() 所以
所以![]() 又
又![]() 所以
所以![]() .
.
所以![]() .
.
(2)由題意,方程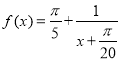 在區間
在區間![]() 上有100個實根,
上有100個實根,
即函數![]() 的圖象與
的圖象與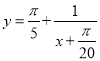 的圖象在區間
的圖象在區間![]() 上有100個交點.
上有100個交點.
由![]() 得
得![]() ,
,
所以![]() 為函數
為函數![]() 的圖象的一個對稱中心.
的圖象的一個對稱中心.
易知![]() 也是函數
也是函數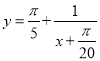 的圖象的對稱中心,
的圖象的對稱中心,
所以![]() 與
與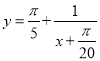 的圖象交點成對出現,且每一對均關于點
的圖象交點成對出現,且每一對均關于點![]() 對稱,
對稱,
所以![]() .
. ![]() ,
,
所以![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn,等比數列{bn}的前n項和為Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通項公式;
(2)若T3=21,求S3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設 A 、B 、Ai ![]() 為集合.
為集合.
(1)滿足 A ∪ B ={a , b}的集合有序對(A , B)有多少對 ? 為什么 ?
(2)滿足 A ∪ B ={a1 , a2 , …, ![]() }的集合有序對(A , B)有多少對? 為什么?
}的集合有序對(A , B)有多少對? 為什么?
(3)滿足![]() 的集合有序組
的集合有序組![]() 有多少組? 為什么 ?
有多少組? 為什么 ?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 設
設![]() 表示p、q中的較大值,
表示p、q中的較大值,![]() 表示p、q中的較小值)記
表示p、q中的較小值)記![]() 的最小值為A,
的最小值為A,![]() 的最大值為B,則A-B=
的最大值為B,則A-B=
A. 16 B. -16 C. a2-2a-16 D. a2+2a-1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)將![]() ,
, ![]() 的方程化為普通方程,并說明它們分別表示什么曲線?
的方程化為普通方程,并說明它們分別表示什么曲線?
(2)以坐標原點為極點,以![]() 軸的正半軸為極軸,建立極坐標系,已知直線
軸的正半軸為極軸,建立極坐標系,已知直線![]() 的極坐標方程為
的極坐標方程為![]() .若
.若![]() 上的點
上的點![]() 對應的參數為
對應的參數為![]() ,點
,點![]() 在
在![]() 上,點
上,點![]() 為
為![]() 的中點,求點
的中點,求點![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,過點![]() 作直線l交拋物線C:
作直線l交拋物線C:![]() 于A,B兩點(點A在P,B之間),設點A,B的縱坐標分別為
于A,B兩點(點A在P,B之間),設點A,B的縱坐標分別為![]() ,
,![]() ,過點A作x軸的垂線交直線
,過點A作x軸的垂線交直線![]() 于點D.
于點D.

(1)求證:![]() ;
;
(2)求![]() 的面積S的最大值.
的面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過隨機詢問72名不同性別的大學生在購買食物時是否看營養說明,得到如下列聯表:
男 | 女 | 總計 | ||
讀營養說明 | 16 | 28 | 44 | |
不讀營養說明 | 20 | 8 | 28 | |
總計 | 36 | 36 | 72 |
(1)根據以上列聯表判斷,能否在犯錯誤的概率不超過0.005的前提下認為性別和是否看營養說明有關系呢?
(2)從被詢問的28名不讀營養說明的大學生中,隨機抽取2名學生,求抽到女生人數![]()
的分布列及數學期望.
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com