
���}Ŀ����֪����(sh��)![]()
��1����(sh��)![]() �ĘOֵ��
�ĘOֵ��
��2�����C�� ![]() ��
��
��3��![]() �����������
�����������![]() ������
������![]() ��������
��������![]() ��ȡֵ������
��ȡֵ������
���𰸡���1��Ҋ������ ��2��![]() .
.
��������ԇ�}��������1�����}�⣬��![]() ���ó�����(sh��)�Ć��{(di��o)�ԣ�������ú���(sh��)�ĘOֵ��
���ó�����(sh��)�Ć��{(di��o)�ԣ�������ú���(sh��)�ĘOֵ��
��2������1��֪![]() �ĘOСֵ������Сֵ���Ƶ�
�ĘOСֵ������Сֵ���Ƶ�![]() ���M(j��n)�����C�ýY(ji��)Փ��
���M(j��n)�����C�ýY(ji��)Փ��
��3�����}��![]() �Ľ���ʽ�����
�Ľ���ʽ�����![]() ����
����![]() �����
�����![]() ������
������![]() ��
�ô���![]() ��ʹ
��ʹ![]() ����
����![]() ��
��![]() ���f�p��
���f�p�� ![]() ��
��![]() ���f������ú���(sh��)��
���f������ú���(sh��)��![]() ����Сֵ�����D(zhu��n)���麯��(sh��)
����Сֵ�����D(zhu��n)���麯��(sh��)![]() �����Ì�(d��o)��(sh��)
�����Ì�(d��o)��(sh��)![]() �Ć��{(di��o)�ԣ�������⌍(sh��)��(sh��)
�Ć��{(di��o)�ԣ�������⌍(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
ԇ�}������
��1����![]() �ɵã�����(sh��)
�ɵã�����(sh��)![]() ��
��![]() �Μp����
�Μp����![]() ���������Ժ���(sh��)
���������Ժ���(sh��)![]() �ĘOֵ��
�ĘOֵ��![]() ȡ�ã���OСֵ
ȡ�ã���OСֵ![]() ��
��
��2������(j��)��1��֪![]() �ĘOСֵ������Сֵ����
�ĘOСֵ������Сֵ����![]() ���Ƶ�
���Ƶ�![]() ��(d��ng)�҃H��(d��ng)
��(d��ng)�҃H��(d��ng)![]() ȡ�ȣ�����
ȡ�ȣ�����![]() ��
��
������
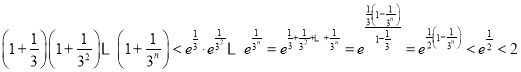
��3��![]() ��
��![]()
��![]() ���t
���t![]() ����
����![]() ��
��![]() ���f��
���f��
��![]() ����(d��ng)
����(d��ng)![]() �r��
�r�� ![]() �����
�����![]() ��ʹ
��ʹ![]() ����
����![]() ��
��![]() ���f�p��
���f�p�� ![]() ��
��![]() ���f��
���f��
��![]() ��
��![]() ����
����![]()
�ߌ��������![]() ������
������![]() ����
����
��![]() ��
��![]()
��![]() ��
��![]() ��
��![]() ����
����![]() ��
�� ![]()
��![]() ��
��![]() ����
����![]() ��
�� ![]() ���@Ȼ
���@Ȼ![]() ��
��![]() ��������
��������![]() ��
�� ![]() ��
��
��![]() ��
��![]() .
.


 �n�nͨ�n�̘�(bi��o)��(zh��n)˼�S�����c����Ӗ(x��n)��ϵ�д�
�n�nͨ�n�̘�(bi��o)��(zh��n)˼�S�����c����Ӗ(x��n)��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���¹ڷ����������g�����˜p������ۼ����������I�ˡ�����.ij���ƽ�_��![]() �^(q��)�S�C(j��)��ȡ��
�^(q��)�S�C(j��)��ȡ��![]() λ�����M(j��n)���{(di��o)�У��@��������ÿ���˽����조�����I�ˡ����M(f��i)�����~����λ��Ԫ���������õ���D��ʾ�l�ʷֲ�ֱ���D.
λ�����M(j��n)���{(di��o)�У��@��������ÿ���˽����조�����I�ˡ����M(f��i)�����~����λ��Ԫ���������õ���D��ʾ�l�ʷֲ�ֱ���D.

��1����![]() ��ֵ��
��ֵ��
��2���ġ������I�ˡ����M(f��i)�����~������![]() Ԫ�ı��{(di��o)�о����У��S�C(j��)��ȡ
Ԫ�ı��{(di��o)�о����У��S�C(j��)��ȡ![]() λ�o�誄Ʒ�����@
λ�o�誄Ʒ�����@![]() λ�������I�ˡ����M(f��i)�����~������
λ�������I�ˡ����M(f��i)�����~������![]() Ԫ�ĸ��ʣ�
Ԫ�ĸ��ʣ�
��3����![]() �^(q��)��
�^(q��)��![]() �f����ԓƽ�_���˴��M(j��n)���M(f��i)���M�����M(f��i)�����~����ƽ��ˮƽһ��ľ���Ͷ��ÿ��
�f����ԓƽ�_���˴��M(j��n)���M(f��i)���M�����M(f��i)�����~����ƽ��ˮƽһ��ľ���Ͷ��ÿ��![]() Ԫ������a(b��)�N.���O(sh��)ÿ�M�еĔ�(sh��)��(j��)��ԓ�M�^(q��)�g�����c(di��n)ֵ���棬ԇ����(j��)�����l�ʷֲ�ֱ���D����Ӌ(j��)ԓƽ�_��
Ԫ������a(b��)�N.���O(sh��)ÿ�M�еĔ�(sh��)��(j��)��ԓ�M�^(q��)�g�����c(di��n)ֵ���棬ԇ����(j��)�����l�ʷֲ�ֱ���D����Ӌ(j��)ԓƽ�_��![]() �^(q��)�MͶ�ŵ�����a(b��)�N�����~.
�^(q��)�MͶ�ŵ�����a(b��)�N�����~.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����������(n��i)���҂������l߅���о��Ľ��c(di��n)�Q�������ε����ģ������ĵ���һ��c(di��n)�ľ��x�ǵ���߅���c(di��n)���x�ăɱ�������Y(ji��)Փ���������F�У��҂�����c(di��n)�c�������ĵ��B���ηQ�������F�ġ��о������������F�ėl�о��Ľ��c(di��n)�Q�����ġ����ġ����t���F���ĵ���c(di��n)�ľ��x�ǵ��������ľ��x��______��![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(j��)���Зl���������Σ��Ѓɽ���У� ��
A.��֪a![]() ��b��2��B��45��B.��֪a��2��b
��b��2��B��45��B.��֪a��2��b![]() ��A��45��
��A��45��
C.��֪b��3��c![]() ��C��60��D.��֪a��2
��C��60��D.��֪a��2![]() ��c��4��A��45��
��c��4��A��45��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ����߅��![]() �У�
�� ![]() ��
�� ![]() ����
����![]() ��
��![]() ����ʹ��ƽ��
����ʹ��ƽ��![]() ƽ��
ƽ��![]() ����D��
����D��

��1�����C�� ![]() ��
��
��2����![]() ��
��![]() ���c(di��n)����ֱ��
���c(di��n)����ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������}������}����(����)
A. ����m��0���t����x2��x��m��0�Ќ�(sh��)��(sh��)�����������}
B. ����e��ȵ�������ȫ�ȡ��ķ����}
C. ����xy��1���tx��y���鵹��(sh��)���������}
D. ����A��B��B���tAB����������}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���タ![]() �Ľ��c(di��n)����
�Ľ��c(di��n)����![]() ��һ�����c(di��n)��
��һ�����c(di��n)�� ![]() ������(bi��o)ԭ�c(di��n)���c(di��n)
������(bi��o)ԭ�c(di��n)���c(di��n)![]() �钁�タ
�钁�タ![]() ������һ�c(di��n)���^�c(di��n)
������һ�c(di��n)���^�c(di��n)![]() ��
��![]() �S��ƽ�о������タ�Ĝ�(zh��n)����
�S��ƽ�о������タ�Ĝ�(zh��n)����![]() ��ֱ��
��ֱ��![]() �����タ���c(di��n)
�����タ���c(di��n)![]() .
.
�������タ![]() �ķ��̣�
�ķ��̣�
�������C��ֱ��![]() �^���c(di��n)
�^���c(di��n)![]() ��������˶��c(di��n)������(bi��o).
��������˶��c(di��n)������(bi��o).
���𰸡���I��![]() ����II���C��Ҋ����.
����II���C��Ҋ����.
��������ԇ�}��������������![]() �����(bi��o)��(zh��n)���̣������
�����(bi��o)��(zh��n)���̣������![]() �Ľ��c(di��n)����(bi��o)�քe��
�Ľ��c(di��n)����(bi��o)�քe��![]() ���ɵ�
���ɵ�![]() ������
������![]() �������タ�ķ��̞�
�������タ�ķ��̞�![]() �����Y(ji��)�ϣ������O(sh��)
�����Y(ji��)�ϣ������O(sh��)![]() ����
���� ���Ķ�ֱ��
���Ķ�ֱ��![]() �ķ��̞�
�ķ��̞�![]() ,(li��n)��ֱ���c���タ���̵�
,(li��n)��ֱ���c���タ���̵�![]() �����
�����![]() ��ֱ��
��ֱ��![]() �ķ��̞�
�ķ��̞� ��������
��������![]() �ķ��̞�
�ķ��̞�![]() ���˕rֱ�����^���c(di��n)
���˕rֱ�����^���c(di��n)![]() .
.
ԇ�}������������������![]() �������(bi��o)��(zh��n)���̿ɵ�
�������(bi��o)��(zh��n)���̿ɵ�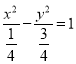 �� ��������
�� ��������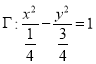 �ǽ��c(di��n)��
�ǽ��c(di��n)��![]() �S�ϵ��p����������
�S�ϵ��p����������![]() ����
����![]() ��
�� ![]() �Ľ��c(di��n)����(bi��o)�քe��
�Ľ��c(di��n)����(bi��o)�քe��![]() ����?y��n)钁�タ�Ľ��c(di��n)����(bi��o)��
����?y��n)钁�タ�Ľ��c(di��n)����(bi��o)��![]() �����}��֪
�����}��֪![]() ������
������![]() �������タ�ķ��̞�
�������タ�ķ��̞�![]() .
.
�������ɣ�����֪���タ![]() �Ĝ�(zh��n)�����̞�
�Ĝ�(zh��n)�����̞�![]() ���O(sh��)
���O(sh��)![]() ���@Ȼ
���@Ȼ![]() .��
.�� ���Ķ�ֱ��
���Ķ�ֱ��![]() �ķ��̞�
�ķ��̞�![]() ,(li��n)��ֱ���c���タ���̵�
,(li��n)��ֱ���c���タ���̵�![]() �����
�����![]()
����(d��ng)![]() ����
����![]() �r��ֱ��
�r��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
����(d��ng)![]() ����
����![]() �r��ֱ��
�r��ֱ��![]() �ķ��̞�
�ķ��̞� ��������
��������![]() �ķ��̞�
�ķ��̞�![]() ���˕rֱ�����^���c(di��n)
���˕rֱ�����^���c(di��n)![]() ��
�� ![]() Ҳ��ֱ��
Ҳ��ֱ��![]() �ķ��̞�
�ķ��̞�![]() �ϣ���ֱ��
�ϣ���ֱ��![]() �ķ��̺��^���c(di��n)
�ķ��̺��^���c(di��n)![]() .
.
���}�͡�����}
���Y(ji��)����
21
���}Ŀ����֪����(sh��)![]() ��
�� ![]()
����(d��ng)![]() �r����(sh��)
�r����(sh��)![]() ���{(di��o)�f�p�^(q��)�g��
���{(di��o)�f�p�^(q��)�g��
������![]() �r���P(gu��n)��
�r���P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��������(sh��)��![]() �M��
�M��![]() ��
�� ![]() ��ӛ
��ӛ![]() ��ǰ
��ǰ![]() �(xi��ng)�͞�
�(xi��ng)�͞�![]() �����C��
�����C�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��1������ƽ����߅��![]() �У���߅��
�У���߅��![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ��
�� ![]() ��
�� ![]() ���c(di��n)
���c(di��n)![]() ��
�� ![]() �քe��
�քe��![]() ��
�� ![]() �����c(di��n)���քe��ֱ��
�����c(di��n)���քe��ֱ��![]() ��
�� ![]() ��
��![]() ��
�� ![]() ���۳���D��2���Ŀ��g���w
���۳���D��2���Ŀ��g���w![]() ��
��
�����������нY(ji��)Փ1��Y(ji��)Փ2���C���� ![]() ��
��![]() ��
��![]() ��
��![]() ���c(di��n)���棻
���c(di��n)���棻
�Y(ji��)Փ1���^���gһ�c(di��n)����ֱ֪���Ĵ��棬���҃H��һ����
�Y(ji��)Փ2���^ƽ���(n��i)һ�lֱ����ԓƽ��Ĵ��棬���҃H��һ����
�����������![]() �Ͷ����
�Ͷ����![]() ����
����![]() ���������F
���������F![]() ���w�e��
���w�e��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ijУ100���W(xu��)�����п�ԇ�Z�ijɿ����l�ʷֲ�ֱ���D��D4��ʾ�����гɿ��ֽM�^(q��)�g�ǣ� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.

��1����D��![]() ��ֵ��
��ֵ��
��2������(j��)�l�ʷֲ�ֱ���D����Ӌ(j��)�@100���W(xu��)���Z�ijɿ���ƽ���֣�
��3�����@100���W(xu��)���Z�ijɿ�ijЩ��?j��n)?sh��)�ε��˔�(sh��)![]() �c��(sh��)�W(xu��)�ɿ�����(y��ng)��?j��n)?sh��)�ε��˔�(sh��)
�c��(sh��)�W(xu��)�ɿ�����(y��ng)��?j��n)?sh��)�ε��˔�(sh��)![]() ֮�����±���ʾ����(sh��)�W(xu��)�ɿ���
֮�����±���ʾ����(sh��)�W(xu��)�ɿ���![]() ֮����˔�(sh��).
֮����˔�(sh��).
��?j��n)?sh��)�� |
|
|
|
|
X:y | 1:1 | 2:1 | 3:4 | 4:5 |
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com