【題目】已知函數(shù)
．
（
）求
的值．
（
）求函數(shù)
的最小正周期和單調(diào)遞增區(qū)間．
【答案】（
）1;（
）
， 
， 
．
【解析】試題分析：(1)根據(jù)函數(shù)
的解析式,計算
的值即可;
(2)化函數(shù)
為正弦型函數(shù),即可求出它的最小正周期與單調(diào)遞增區(qū)間.
試題解析：（
）∵函數(shù)
，
∴
．
（
）由（
）知
，
∴函數(shù)
的最小正周期
，
令
， 
，
得
， 
，
∴函數(shù)
的單調(diào)遞增區(qū)間是
， 
．
點睛:三角函數(shù)式的化簡要遵循“三看”原則:（1）一看“角”，這是最重要的一環(huán)，通過看角之間的區(qū)別和聯(lián)系，把角進行合理的拆分，從而正確使用公式；（2）而看“函數(shù)名稱”看函數(shù)名稱之間的差異，從而確定使用公式，常見的有“切化弦”；（3）三看“結(jié)構(gòu)特征”，分析結(jié)構(gòu)特征，可以幫助我們找到變形的方向，如“遇到分式通分”等.
開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案
名題訓(xùn)練系列答案
期末集結(jié)號系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，定義在［－1,+∞)上的函數(shù)
的圖象由一條線段及拋物線的一部分組成．
(1)求
的值及的解析式；
(2)若f（x）=
，求實數(shù)x的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
經(jīng)過點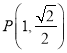
，且兩焦點與短軸的一個端點的連線構(gòu)成等腰直角三角形．
（
）求橢圓的方程．
（
）過定點
的動直線
，交橢圓
于
、
兩點，試問：在坐標(biāo)平面上是否存在一個定點
，使得以
為直徑的圓恒過點
．若存在，求出點
的坐標(biāo)；若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）=
的定義域為M．
（1）求M；
（2）當(dāng)x∈M時，求g（x）=4x﹣2x+1+1的值域．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若f（x）是定義在（﹣∞，+∞）上的偶函數(shù)，x1 ， x2∈[0，+∞）（x1≠x2），有 
，則（ ）
A.f（3）＜f（1）＜f（﹣2）
B.f（1）＜f（﹣1）＜f（3）
C.f（﹣2）＜f（1）＜f（3）
D.f（3）＜f（﹣2）＜f（1）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在△ABC中，角A、B、C所對的邊分別為a，b，c．已知a+c=3 
，b=3．
（1）求cosB的最小值；
（2）若 
=3，求A的大小．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在如圖所示的幾何體中，四邊形
是正方形， 
平面， 
分別為
的中點，且
.
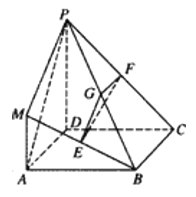
（1）求證：平面
平面
；
（2）求證：平面
平面
；
（3）求三棱錐
與四棱錐
的體積之比.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
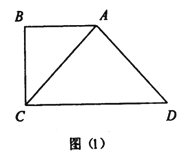
【題目】已知直角梯形
，如圖（1）所示， 
， 
， 
， 
，連接
，將
沿
折起，使得平面
平面
，得到幾何體
，如圖（2）所示.
（1）求證： 
平面
；
（2）若
，求二面角
的大小.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
