
���}Ŀ����֪����(sh��)![]() ��
��![]() �錍(sh��)����(sh��)��
�錍(sh��)����(sh��)��![]() ����
����
����(d��ng)![]() �r(sh��)��
�r(sh��)��
���O(sh��)![]() ���Дຯ��(sh��)
���Дຯ��(sh��)![]() ����ż�ԣ����f�����ɣ�
����ż�ԣ����f�����ɣ�
�����C������(sh��)![]() ��
��![]() ����������(sh��)��
����������(sh��)��
�����O(sh��)����![]() ����
����![]() ����
����![]() ��ȡֵ��������
��ȡֵ��������![]() ��ʾ����
��ʾ����
���𰸡���������Ҋ��������Ҋ������������![]()
��������
�������_������(sh��)�Ľ���ʽ��Ȼ�����ú���(sh��)�Ķ��x��g��-x��=g��x��,g�Дຯ��(sh��)����ż�ԣ������ö��κ���(sh��)�c��(f��)�Ϻ���(sh��)�Ć��{(di��o)�Ե������C�ú���(sh��)�Ć��{(di��o)��
����ԭ���}�D(zhu��n)���������Ć��}���Y(ji��)�Ϻ�����ėl��������Ì�(sh��)��(sh��)�˵ķ�����
������������(sh��)��ż����(sh��)���C�����£�
��(d��ng)a=1��b=3�r(sh��)��![]() ����g(x)��f(x+2)��
����g(x)��f(x+2)��![]() ��
��
�䶨�x��?y��n)?/span>{x|x��1��x��-1}������(sh��)�Ķ��x���P(gu��n)������(bi��o)ԭ�c(di��n)���Q��
g(-x)=![]() =g(x),��g��x����ż����(sh��).
=g(x),��g��x����ż����(sh��).
��![]() ��
��
��u��x��=![]() ��
��
��֪u��x����![]() ����������(sh��)��u��x����ֵ��?y��n)?/span>[-1,0), f��u��=
����������(sh��)��u��x����ֵ��?y��n)?/span>[-1,0), f��u��=![]() ��[-1,0)��������(sh��)����
��[-1,0)��������(sh��)����![]() ��
��![]() ����������(sh��).
����������(sh��).
������?y��n)?/span>M��N=�����Ժ���(sh��)y=f��x���cy=![]() �ĈD��o�����c(di��n)��
�ĈD��o�����c(di��n)��
������![]() ���~���o�o��(sh��)��,
���~���o�o��(sh��)��,
![]() ,
,
��(d��ng)��=0�r(sh��),���̟o�⣬�@Ȼ�����}����
��(d��ng)�ˡ�0�r(sh��)����y��(xa)(xb)![]() =
=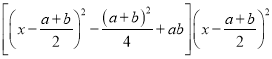 ��
��
��t=![]() ���ty=
���ty=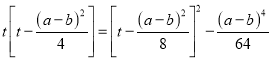 ��
��
��(d��ng)t=![]() �r(sh��)��ymin=
�r(sh��)��ymin=![]() ��
��
���ԣ�Ҫʹ���~���o��(sh��)��(sh��)�⣬ֻҪ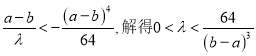 ��
��
�C����![]()


 �eһ����ͬ�����v����ϵ�д�
�eһ����ͬ�����v����ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��2019���ʮ����Ů�����籭��12֧��ِ���(du��)����ِِ���ȡ��ѭ�h(hu��n)��ʽ����ÿ֧���(du��)�M(j��n)��11����ِ����e���x������܊���e��Ҏ(gu��)�t���£���ِ��ȡ5��3���ƣ�����ِ����3��0��3��1ȡ�ٵ����(du��)�e3�֣�ؓ(f��)�(du��)�e0�֣����ڱ�ِ����3��2ȡ�ٵ����(du��)�e2�֣�ؓ(f��)�(du��)�e1�֣�9݆�^�e�ְ��ϵ�ǰ2���քe���Ї��(du��)�������(du��)���Ї��(du��)�e26�֣������(du��)�e22�֣���10݆�Ї��(du��)���������S���(du��)���O(sh��)ÿ�ֱ�ِ�Ї��(du��)ȡ�ٵĸ��ʞ�![]() ��
��
��1����10݆��ِ�У�ӛ�Ї��(du��)3��1ȡ�ٵĸ��ʞ�![]() ����
����![]() �����ֵ�c(di��n)
�����ֵ�c(di��n)![]() ��
��
��2���ԣ�1���е�![]() ����
����![]() ��ֵ��
��ֵ��
��i���ڵ�10݆��ِ�У��Ї��(du��)���÷e�֞�![]() ����
����![]() �ķֲ��У�
�ķֲ��У�
��������֪��10݆�����(du��)�e3�֣��Д��Ї��(du��)�ܷ���ǰһ݆�Z�ù�܊����10݆�^�oՓ���һ݆����11݆�Y(ji��)����Σ��Ї��(du��)�e����ࣩ�����ܣ��������(y��ng)�ĸ��ʣ������ܣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڡ�ABC�У���A��B��C����߅�քe��a��b��c.��![]() ��c��6���t��ABC��ӈA�İ돽��С��_____.
��c��6���t��ABC��ӈA�İ돽��С��_____.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
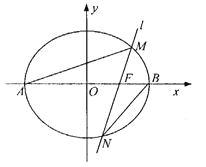
���}Ŀ����֪F(0,1)��ƽ����һ�c(di��n)��H��ֱ��l��y=��1������һ�c(di��n)���^�c(di��n)H��ֱ��l�Ĵ���m���O(sh��)����FH���д����cֱ��m�����c(di��n)P��ӛ�c(di��n)P��܉�E����.
��1����܉�E���ķ��̣�
��2���^�c(di��n)F�����ഹֱ��ֱ��AB�cCD������ֱ��AB�c܉�E�������c(di��n)AB��ֱ��CD�c܉�E�������c(di��n)CD���O(sh��)�c(di��n)M��N�քe��AB��CD�����c(di��n).
�ن�ֱ��MN�Ƿ���^���c(di��n)�������(j��ng)�^���c(di��n)�����ԓ���c(di��n)����t�f�����ɣ�
�����FMN����e����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ژO����(bi��o)ϵ�У���֪�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��3.
�ľ��x��3.
��1����(sh��)��(sh��)![]() ��ֵ��
��ֵ��
��2���O(sh��)![]() ��ֱ��
��ֱ��![]() �ϵĄ�(d��ng)�c(di��n)��
�ϵĄ�(d��ng)�c(di��n)��![]() �ھ���
�ھ���![]() �ϣ��ҝM��
�ϣ��ҝM��![]() �����c(di��n)
�����c(di��n)![]() ܉�E���̣���ָ��܉�E��ʲô�D��.
܉�E���̣���ָ��܉�E��ʲô�D��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����������![]() �У�����
�У�����![]() �ǵ������Σ�
�ǵ������Σ�![]() ����c(di��n)
����c(di��n)![]() �ڵ���
�ڵ���![]() ��(n��i)����Ӱǡ���c(di��n)
��(n��i)����Ӱǡ���c(di��n)![]() ��
��
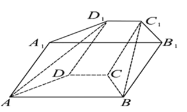
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() �c����
�c����![]() ���ɵĽǞ�
���ɵĽǞ�![]() ����ƽ��
����ƽ��![]() �cƽ��
�cƽ��![]() �����J����ǵ�����ֵ��
�����J����ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����������̄�(w��)��l(f��)չ��ͬ�r(sh��)Ҳ�O��ش��M(j��n)�˿��f�ИI(y��)�İl(f��)չ�����˸��õط���(w��)�͑���ij���f��˾ʹ�ÿ͑��u�r(ji��)ϵ�y(t��ng)�����f����(w��)�ˆT�ķ���(w��)�M(j��n)���u�r(ji��)��ÿ�¸���(j��)�͑��u�r(ji��)�u�x�������f֮��������֪�����fС����С��?ji��n)�ÿ��(g��)�±��u�x�������f֮�����ĸ��ʶ���![]() ���tС��?ji��n)ڵ�һ���ȵ?/span>3��(g��)������2��(g��)�¶����u�������f֮�����ĸ��ʞ�_______���O(sh��)С��?ji��n)��ϰ���?/span>6��(g��)���б��u�������f֮�����ĴΔ�(sh��)���S�C(j��)׃��X���t�S�C(j��)׃��X�ķ���
���tС��?ji��n)ڵ�һ���ȵ?/span>3��(g��)������2��(g��)�¶����u�������f֮�����ĸ��ʞ�_______���O(sh��)С��?ji��n)��ϰ���?/span>6��(g��)���б��u�������f֮�����ĴΔ�(sh��)���S�C(j��)׃��X���t�S�C(j��)׃��X�ķ���![]() ______��
______��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������
������![]() .
.
��������(d��ng)![]() �r(sh��)���Дຯ��(sh��)
�r(sh��)���Дຯ��(sh��)![]() �����c(di��n)��(g��)��(sh��)��
�����c(di��n)��(g��)��(sh��)��
������������![]() ��
��![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪�E�A![]() �^�c(di��n)
�^�c(di��n)![]() ���x���ʞ�
���x���ʞ�![]() ��
��![]() �քe�ǙE�A
�քe�ǙE�A![]() ��������c(di��n)���^�ҽ��c(di��n)
��������c(di��n)���^�ҽ��c(di��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ���c(di��n)��
���c(di��n)��
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2��ӛ![]() ��
��![]() ����e�քe��
����e�քe��![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
��3��ӛֱ��![]() ��
��![]() ��б�ʷքe��
��б�ʷքe��![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com