
【題目】在△ABC中,角A,B,C所對邊分別為a,b,c.若![]() ,c=6,則△ABC外接圓的半徑大小是_____.
,c=6,則△ABC外接圓的半徑大小是_____.
【答案】![]()
【解析】
由題意結合三角函數恒等變換、正弦定理可得sinBcosC=sinBsinC,結合sinB>0,可求tanC=1,結合范圍C∈(0,π),可求![]() ,設△ABC外接圓的半徑大小為R,根據正弦定理即可求解△ABC外接圓的半徑,即可得解.
,設△ABC外接圓的半徑大小為R,根據正弦定理即可求解△ABC外接圓的半徑,即可得解.
由條件知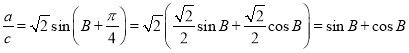 ,
,
根據正弦定理得:![]() ,
,
所以sinA=sinC(sinB+cosB)=sinCsinB+sinCcosB,
又sinA=sin(B+C)=sinBcosC+cosBsinC,
于是sinBcosC=sinBsinC,
因為sinB>0,所以cosC=sinC即tanC=1,
又C∈(0,π),所以![]() ,
,
設△ABC外接圓的半徑大小為R,根據正弦定理得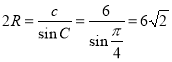 ,
,
因此![]() .
.
故答案為:![]() .
.


科目:高中數學 來源: 題型:
【題目】近年來,共享單車在我國各城市迅猛發展,為人們的出行提供了便利,但也給城市的交通管理帶來了一些困難,為掌握共享單車在![]() 省的發展情況,某調查機構從該省抽取了5個城市,并統計了共享單車的
省的發展情況,某調查機構從該省抽取了5個城市,并統計了共享單車的![]() 指標
指標![]() 和
和![]() 指標
指標![]() ,數據如下表所示:
,數據如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)試求![]() 與
與![]() 間的相關系數
間的相關系數![]() ,并說明
,并說明![]() 與
與![]() 是否具有較強的線性相關關系(若
是否具有較強的線性相關關系(若![]() ,則認為
,則認為![]() 與
與![]() 具有較強的線性相關關系,否則認為沒有較強的線性相關關系).
具有較強的線性相關關系,否則認為沒有較強的線性相關關系).
(2)建立![]() 關于
關于![]() 的回歸方程,并預測當
的回歸方程,并預測當![]() 指標為7時,
指標為7時,![]() 指標的估計值.
指標的估計值.
(3)若某城市的共享單車![]() 指標
指標![]() 在區間
在區間![]() 的右側,則認為該城市共享單車數量過多,對城市的交通管理有較大的影響交通管理部門將進行治理,直至
的右側,則認為該城市共享單車數量過多,對城市的交通管理有較大的影響交通管理部門將進行治理,直至![]() 指標
指標![]() 在區間
在區間![]() 內現已知
內現已知![]() 省某城市共享單車的
省某城市共享單車的![]() 指標為13,則該城市的交通管理部門是否需要進行治理?試說明理由.
指標為13,則該城市的交通管理部門是否需要進行治理?試說明理由.
參考公式:回歸直線![]() 中斜率和截距的最小二乘估計分別為
中斜率和截距的最小二乘估計分別為
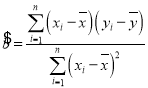 ,,
,,![]() 相關系數
相關系數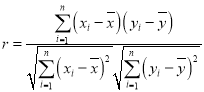
參考數據: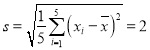 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的點,
上的點,![]() ,且
,且![]() (如圖①).將四邊形
(如圖①).將四邊形![]() 沿
沿![]() 折起,連接
折起,連接![]() 、
、![]() 、
、![]() (如圖②).在折起的過程中,則下列表述:
(如圖②).在折起的過程中,則下列表述:

①![]() 平面
平面![]() ;
;
②四點![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,則平面
,則平面![]() 平面
平面![]() ;
;
④平面![]() 與平面
與平面![]() 可能垂直.其中正確的是__________.
可能垂直.其中正確的是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
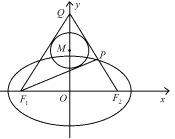
【題目】如圖,已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 軸的正半軸上一點,
軸的正半軸上一點,![]() 交橢圓于
交橢圓于![]() ,且
,且![]() ,
,![]() 的內切圓
的內切圓![]() 半徑為1.
半徑為1.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 點為圓
點為圓![]() 上一點,求
上一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)為偶函數,且y=f(x)圖象的兩相鄰對稱軸間的距離為
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)為偶函數,且y=f(x)圖象的兩相鄰對稱軸間的距離為![]() ,則f(
,則f(![]() )的值為( )
)的值為( )
A.﹣1B.1C.![]() .D.
.D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為實常數且
為實常數且![]() ).
).
(Ⅰ)當![]() 時;
時;
①設![]() ,判斷函數
,判斷函數![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
②求證:函數![]() 在
在![]() 上是增函數;
上是增函數;
(Ⅱ)設集合![]() ,若
,若![]() ,求
,求![]() 的取值范圍(用
的取值范圍(用![]() 表示).
表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
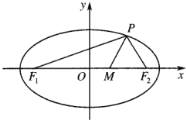
【題目】已知橢圓![]() 的左、右焦點分別是
的左、右焦點分別是![]() ,
,![]() ,點
,點![]() 是橢圓
是橢圓![]() 上除長軸端點外的任一點,連接
上除長軸端點外的任一點,連接![]() ,
,![]() ,設
,設![]() 的內角平分線
的內角平分線![]() 交
交![]() 的長軸于點
的長軸于點![]() .
.
(Ⅰ)求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com