Question

【題目】設函數(shù)定義域為，對于區(qū)間，如果存在，，使得，則稱區(qū)間為函數(shù)的區(qū)間.

（Ⅰ）判斷是否是函數(shù)的區(qū)間;

（Ⅱ）若是函數(shù)（其中）的區(qū)間，求的取值范圍;

（Ⅲ）設為正實數(shù)，若是函數(shù)的區(qū)間，求的取值范圍.

Answer 1

【答案】（Ⅰ）見證明；（Ⅱ） （Ⅲ）

【解析】

Ⅰ根據新定義，即可求出判斷，

Ⅱ根據新定義和對數(shù)函數(shù)的性質，即可求出a的取值范圍，

Ⅲ根據新定義和余弦函數(shù)的性質可得存在k，，使得，再分類討論即可求出的取值范圍

（Ⅰ）不是函數(shù)的區(qū)間，理由如下：

因為 對，，

所以 .

所以 均有，

即不存在，，使得.

所以不是函數(shù)的區(qū)間

（Ⅱ）由是函數(shù)（其中的區(qū)間，可知

存在，，使得.

所以 .

因為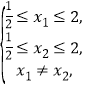

所以 ，即.

又因為 且，

所以 .

（Ⅲ）因為 是函數(shù)的區(qū)間，

所以 存在，，使得.

所以

所以 存在，使得

不妨設. 又因為 ，

所以 .

所以 .

即在區(qū)間內存在兩個不同的偶數(shù).

①當時，區(qū)間的長度，

所以 區(qū)間內必存在兩個相鄰的偶數(shù)，故符合題意.

②當時，有，

所以 .

（i）當時，有即.

所以 也符合題意.

（ii）當時，有即.

所以 符合題意.

（iii）當時，有即此式無解.

綜上所述，的取值范圍是.