
【題目】在邊長為8的正方形ABCD中,M是BC的中點,N是AD邊上的一點,且DN=3NA,若對于常數m,在正方形ABCD的邊上恰有6個不同的點P,使![]() ,則實數m的取值范圍是_______.
,則實數m的取值范圍是_______.
科目:高中數學 來源: 題型:
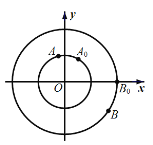
【題目】如圖,點![]() 分別是圓心在原點,半徑為
分別是圓心在原點,半徑為![]() 和
和![]() 的圓上的動點.動點
的圓上的動點.動點![]() 從初始位置
從初始位置![]() 開始,按逆時針方向以角速度
開始,按逆時針方向以角速度![]() 作圓周運動,同時點
作圓周運動,同時點![]() 從初始位置
從初始位置![]() 開始,按順時針方向以角速度
開始,按順時針方向以角速度![]() 作圓周運動.記
作圓周運動.記![]() 時刻,點
時刻,點![]() 的縱坐標分別為
的縱坐標分別為![]() .
.
(Ⅰ)求![]() 時刻,
時刻,![]() 兩點間的距離;
兩點間的距離;
(Ⅱ)求![]() 關于時間
關于時間![]() 的函數關系式,并求當
的函數關系式,并求當![]() 時,這個函數的值域.
時,這個函數的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() ,直線l不過原點O且不平行于坐標軸,l與E有兩個交點A,B,線段AB的中點為M.
,直線l不過原點O且不平行于坐標軸,l與E有兩個交點A,B,線段AB的中點為M.
![]() 若
若![]() ,點K在橢圓E上,
,點K在橢圓E上,![]() 、
、![]() 分別為橢圓的兩個焦點,求
分別為橢圓的兩個焦點,求![]() 的范圍;
的范圍;
![]() 證明:直線OM的斜率與l的斜率的乘積為定值;
證明:直線OM的斜率與l的斜率的乘積為定值;
![]() 若l過點
若l過點![]() ,射線OM與橢圓E交于點P,四邊形OAPB能否為平行四邊形?若能,求此時直線l斜率;若不能,說明理由.
,射線OM與橢圓E交于點P,四邊形OAPB能否為平行四邊形?若能,求此時直線l斜率;若不能,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設直線l:![]() ,圓C:
,圓C:![]() ,則下列說法中正確的是( )
,則下列說法中正確的是( )
A.直線l與圓C有可能無公共點
B.若直線l的一個方向向量為![]() ,則
,則![]()
C.若直線l平分圓C的周長,則![]()
D.若直線l與圓C有兩個不同交點M、N,則線段MN的長的最小值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某鄉鎮政府為了解決農村教師的住房問題,計劃征用一塊土地蓋一幢建筑總面積為10000![]() 公寓樓(每層的建筑面積相同).已知士地的征用費為
公寓樓(每層的建筑面積相同).已知士地的征用費為![]() ,土地的征用面積為第一層的
,土地的征用面積為第一層的![]() 倍,經工程技術人員核算,第一層建筑費用為
倍,經工程技術人員核算,第一層建筑費用為![]() ,以后每增高一層,其建筑費用就增加
,以后每增高一層,其建筑費用就增加![]() ,設這幢公寓樓高層數為n,總費用為
,設這幢公寓樓高層數為n,總費用為![]() 萬元.(總費用為建筑費用和征地費用之和)
萬元.(總費用為建筑費用和征地費用之和)
(1)若總費用不超過835萬元,求這幢公寓樓最高有多少層數?
(2)試設計這幢公寓的樓層數,使總費用最少,并求出最少費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正數數列![]() 、
、![]() 滿足:
滿足:![]() ≥
≥![]() ,且對一切k≥2,k
,且對一切k≥2,k![]() ,
,![]() 是
是![]() 與
與![]() 的等差中項,
的等差中項,![]() 是
是![]() 與
與![]() 的等比中項.
的等比中項.
(1)若![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)求證:![]() 是等差數列的充要條件是
是等差數列的充要條件是![]() 為常數數列;
為常數數列;
(3)記![]() ,當n≥2(n
,當n≥2(n![]() )時,指出
)時,指出![]() 與
與![]() 的大小關系并說明理由.
的大小關系并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四邊形![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上(不為端點),且滿足
上(不為端點),且滿足![]() ,其中
,其中![]() .
.

(1)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成的角的大小;
所成的角的大小;
(2)是否存在![]() ,使
,使![]() 是
是![]() 的公垂線,即
的公垂線,即![]() 同時垂直
同時垂直![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位: ![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近8年的年宣傳費
(單位:千元)的影響,對近8年的年宣傳費![]() 和年銷售量
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.

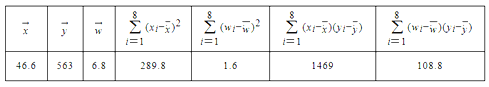
表中![]() ,
,![]() .
.
(1)根據散點圖判斷, ![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)已知這種產品的年利潤![]() 與
與![]() 、
、![]() 的關系為
的關系為![]() .根據(2)的結果要求:年宣傳費
.根據(2)的結果要求:年宣傳費![]() 為何值時,年利潤最大?
為何值時,年利潤最大?
附:對于一組數據![]() ,
, ![]() ,…,
,…, ![]() 其回歸直線
其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為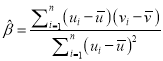 ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com