【題目】已知橢圓
（
）的上頂點(diǎn)與拋物線
（
）的焦點(diǎn)
重合.
（1）設(shè)橢圓和拋物線交于
， 
兩點(diǎn)，若
，求橢圓的方程；
（2）設(shè)直線
與拋物線和橢圓均相切，切點(diǎn)分別為
， 
，記
的面積為
，求證： 
.
【答案】(1) 
(2)見(jiàn)解析
【解析】試題分析：（1）根據(jù)橢圓幾何性質(zhì)得p，再根據(jù)對(duì)稱(chēng)性得A坐標(biāo)，代人橢圓方程可得a,（2）先根據(jù)導(dǎo)數(shù)幾何意義得拋物線切線方程，再與橢圓方程聯(lián)立，根據(jù)判別式為零確定切點(diǎn)，根據(jù)三角形面積公式表示面積，最后根據(jù)基本不等式求最值，證得結(jié)論.
試題解析：（1）易知
，則拋物線的方程為
由
及圖形的對(duì)稱(chēng)性，不妨設(shè)
，
代入
，得
，則
.
將之代入橢圓方程得
，得
，
所以橢圓的方程為
.
（2）設(shè)切點(diǎn)
， 
即
，求導(dǎo)得
，則切線
的斜率為
，方程
，即
，
將之與橢圓
聯(lián)立得
，
令判別式
化簡(jiǎn)整理得
， 
，此時(shí)
設(shè)直線
與
軸交于點(diǎn)
，則
由基本不等式得
， 
則
，僅當(dāng)
時(shí)取等號(hào)，但此時(shí)
，故等號(hào)無(wú)法取得，于是
.
一諾書(shū)業(yè)暑假作業(yè)快樂(lè)假期云南美術(shù)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，已知圓
，點(diǎn)
是圓
上任意一點(diǎn)，線段
的垂直平分線和半徑
相交于
.
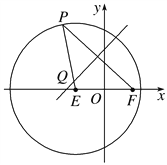
(1)求動(dòng)點(diǎn)
的軌跡
的方程；
(2)已知
是軌跡
的三個(gè)動(dòng)點(diǎn)，點(diǎn)
在一象限， 
與
關(guān)于原點(diǎn)對(duì)稱(chēng)，且
，問(wèn)
的面積是否存在最小值？若存在，求出此最小值及相應(yīng)直線
的方程；若不存在，請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】給定點(diǎn)
，若
是直線
上位于第一象限內(nèi)的一點(diǎn)，直線
與
軸的正半軸相交于點(diǎn)
.試探究：
的面積是否具有最小值?若有，求出點(diǎn)的坐標(biāo)；若沒(méi)有，則說(shuō)明理由.若點(diǎn)為直線
上的任意一點(diǎn)，情況又會(huì)怎樣呢?
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】由國(guó)家公安部提出，國(guó)家質(zhì)量監(jiān)督檢驗(yàn)檢疫總局發(fā)布的《車(chē)輛駕駛?cè)藛T血液、呼氣酒精含量閥值與檢驗(yàn)標(biāo)準(zhǔn)（
）》于
年
月
日正式實(shí)施.車(chē)輛駕駛?cè)藛T酒飲后或者醉酒后駕車(chē)血液中的酒精含量閥值見(jiàn)表.經(jīng)過(guò)反復(fù)試驗(yàn)，一般情況下，某人喝一瓶啤酒后酒精在人體血液中的變化規(guī)律的“散點(diǎn)圖”見(jiàn)圖，
喝瓶啤酒的情況
且圖表示的函數(shù)模型
，則該人喝一瓶啤酒后至少經(jīng)過(guò)多長(zhǎng)時(shí)間才可以駕車(chē)（時(shí)間以整小時(shí)計(jì)算）？（參考數(shù)據(jù)：
，
）
（ ）
駕駛行為類(lèi)型 | 閥值 |
飲酒后駕車(chē) |
|
醉酒后駕車(chē) |
|
車(chē)輛駕車(chē)人員血液酒精含量閥值
A.
B.
C.D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】提升城市道路通行能力，可為市民提供更多出行便利.我校某研究性學(xué)習(xí)小組對(duì)成都市一中心路段(限行速度為
千米/小時(shí))的擁堵情況進(jìn)行調(diào)查統(tǒng)計(jì)，通過(guò)數(shù)據(jù)分析發(fā)現(xiàn)：該路段的車(chē)流速度
(輛/千米)與車(chē)流密度
(千米/小時(shí))之間存在如下關(guān)系:如果車(chē)流密度不超過(guò)
該路段暢通無(wú)阻(車(chē)流速度為限行速度)；當(dāng)車(chē)流密度在
時(shí)，車(chē)流速度是車(chē)流密度的一次函數(shù)；車(chē)流密度一旦達(dá)到
該路段交通完全癱瘓(車(chē)流速度為零).
（1）求
關(guān)于的函數(shù)
（2）已知車(chē)流量(單位時(shí)間內(nèi)通過(guò)的車(chē)輛數(shù))等于車(chē)流密度與車(chē)流速度的乘積，求此路段車(chē)流量的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】甲同學(xué)寫(xiě)出三個(gè)不等式：
:
，
:
，
：
，然后將
的值告訴了乙、丙、丁三位同學(xué)，要求他們各用一句話(huà)來(lái)描述，以下是甲、乙、丙、丁四位同學(xué)的描述：
乙：為整數(shù)；
丙：是成立的充分不必要條件；
丁：是成立的必要不充分條件；
甲：三位同學(xué)說(shuō)得都對(duì)，則的值為__________．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
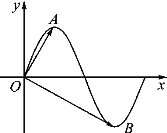
【題目】已知函數(shù)
(
>0)的部分圖象如圖所示，A，B分別是這部分圖象上的最高點(diǎn)、最低點(diǎn)，
為坐標(biāo)原點(diǎn)，若
·
＝0，
則下列結(jié)論：①函數(shù)
是周期為4的奇函數(shù)；②函數(shù)
是周期為4的偶函數(shù)；③函數(shù)
的最大值是
；④函數(shù)向左平移
個(gè)單位后得到的函數(shù)圖象關(guān)于原點(diǎn)對(duì)稱(chēng)；其中錯(cuò)誤命題的個(gè)數(shù)是（ ）
A.3B.2C.1D.0
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】某企業(yè)有甲、乙兩套設(shè)備生產(chǎn)同一種產(chǎn)品，為了檢測(cè)兩套設(shè)備的生產(chǎn)質(zhì)量情況，隨機(jī)從兩套設(shè)備生產(chǎn)的大量產(chǎn)品中各抽取了50件產(chǎn)品作為樣本，檢測(cè)一項(xiàng)質(zhì)量指標(biāo)值，若該項(xiàng)質(zhì)量指標(biāo)值落在
內(nèi)，則為合格品，否則為不合格品. 表1是甲套設(shè)備的樣本的頻數(shù)分布表，圖1是乙套設(shè)備的樣本的頻率分布直方圖.
表1：甲套設(shè)備的樣本的頻數(shù)分布表
質(zhì)量指標(biāo)值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數(shù) | 1 | 4 | 19 | 20 | 5 | 1 |
圖1：乙套設(shè)備的樣本的頻率分布直方圖
（1）填寫(xiě)下面列聯(lián)表，并根據(jù)列聯(lián)表判斷是否有90%的把握認(rèn)為該企業(yè)生產(chǎn)的這種產(chǎn)品的質(zhì)量指標(biāo)值與甲、乙兩套設(shè)備的選擇有關(guān)；
