Question

【題目】如圖1，2，在Rt△ABC中，AB=BC=4，點E在線段AB上，過點E作交AC于點F，將△AEF沿EF折起到△PEF的位置（點A與P重合），使得∠PEB=60°．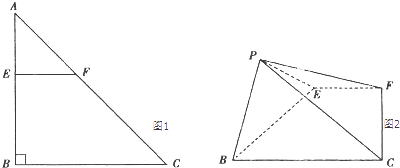

（1）求證：EF⊥PB；
（2）試問：當點E在何處時，四棱錐P﹣EFCB的側面的面積最大？并求此時四棱錐P﹣EFCB的體積及直線PC與平面EFCB所成角的正切值．

Answer 1

【答案】
（1）證明：∵EF∥BC且BC⊥AB，

∴EF⊥AB，即EF⊥BE，EF⊥PE．又BE∩PE=E，

∴EF⊥平面PBE，又PB平面PBE，

∴EF⊥PB

（2）解：設BE=x，PE=y，則x+y=4．

∴ ．

當且僅當x=y=2時，S△PEB的面積最大，此時，BE=PE=2．

由（1）知EF⊥平面PBE，

∵EF平面EFCB，∴平面EFCB⊥平面PBE．

在平面PBE中，作PO⊥BE于O，則PO⊥平面EFCB．

即PO為四棱錐P﹣EFCB的高．

又 ．

∴

∵ ，

∴BO=1，在Rt△OBC中， ．

∵PO⊥平面EFCB，∴∠PCO就是PC與平面EFCB所成角．

∴ ，

故直線PC與平面EFCB所成角的正切值為

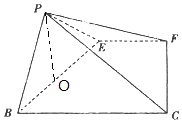
【解析】（1）推導出EF⊥AB，EF⊥BE，EF⊥PE，由此能證明EF⊥PB．　（2）設BE=x，PE=y，則x+y=4，當且僅當x=y=2時，S△PEB的面積最大，此時，BE=PE=2．EF⊥平面PBE，從而平面EFCB⊥平面PBE．作PO⊥BE于O，則PO為四棱錐P﹣EFCB的高，∠PCO就是PC與平面EFCB所成角．由此能求出結果．