
【題目】(12分)
煉鋼是一個氧化降碳的過程,由于鋼水含碳量的多少直接影響冶煉時間的長短,因此必須掌握鋼水含碳量和冶煉時間的關(guān)系.現(xiàn)已測得爐料熔化完畢時鋼水的含碳量x與冶煉時間y(從爐料熔化完畢到出鋼的時間)的一組數(shù)據(jù),如下表所示:

(1)據(jù)統(tǒng)計表明,![]() 之間具有線性相關(guān)關(guān)系,請用相關(guān)系數(shù)r加以說明(
之間具有線性相關(guān)關(guān)系,請用相關(guān)系數(shù)r加以說明(![]()
![]() ,則認(rèn)為y與x有較強(qiáng)的線性相關(guān)關(guān)系,否則認(rèn)為沒有較強(qiáng)的線性相關(guān)關(guān)系,r精確到0.001);
,則認(rèn)為y與x有較強(qiáng)的線性相關(guān)關(guān)系,否則認(rèn)為沒有較強(qiáng)的線性相關(guān)關(guān)系,r精確到0.001);
(2)建立y關(guān)于x的回歸方程(回歸系數(shù)的結(jié)果精確到0.01);
(3)根據(jù)(2)中的結(jié)論,預(yù)測鋼水含碳量為160個0.01%的冶煉時間.
參考公式:回歸方程![]() 中斜率和截距的最小二乘估計分別為
中斜率和截距的最小二乘估計分別為 ,
,
![]() ,相關(guān)系數(shù)
,相關(guān)系數(shù)
參考數(shù)據(jù): ,
,
![]() .
.
【答案】(1)可以認(rèn)為y與x有較強(qiáng)的線性相關(guān)關(guān)系.
(2)![]() .
.
(3)大約需要![]() .
.
【解析】分析:(1)由相關(guān)系數(shù)的公式,可求得![]() 的值,即可認(rèn)為
的值,即可認(rèn)為![]() 與
與![]() 有較強(qiáng)的線性相關(guān)關(guān)系;
有較強(qiáng)的線性相關(guān)關(guān)系;
(2)由回歸系數(shù)的公式求得![]() 的值,進(jìn)而得到
的值,進(jìn)而得到![]() ,即可得到回歸直線方程;
,即可得到回歸直線方程;
(3)代入![]() ,求得
,求得![]() 的值,即可得到預(yù)測.
的值,即可得到預(yù)測.
解析:(1)由題意![]() ,
,
所以可以認(rèn)為![]() 與
與![]() 有較強(qiáng)的線性相關(guān)關(guān)系;
有較強(qiáng)的線性相關(guān)關(guān)系;
(2)因為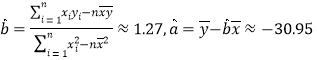 ,
,
所以回歸直線方程為![]() .
.
(3)當(dāng)![]() 時,
時,![]() ,
,
即大約需要冶煉![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】通過隨機(jī)詢問![]() 名不同性別的大學(xué)生在購買食物時是否看營養(yǎng)說明,得到如下列聯(lián)表:
名不同性別的大學(xué)生在購買食物時是否看營養(yǎng)說明,得到如下列聯(lián)表:
男 | 女 | 總計 | |
讀營養(yǎng)說明 |
|
|
|
不讀營養(yǎng)說明 |
|
|
|
總計 |
|
|
|
附:
|
|
|
|
|
|
|
|
![]()
(1)由以上列聯(lián)表判斷,能否在犯錯誤的概率不超過![]() 的前提下認(rèn)為性別和是否看營養(yǎng)說明有關(guān)系呢?
的前提下認(rèn)為性別和是否看營養(yǎng)說明有關(guān)系呢?
(2)從被詢問的![]() 名不讀營養(yǎng)說明的大學(xué)生中隨機(jī)選取
名不讀營養(yǎng)說明的大學(xué)生中隨機(jī)選取![]() 名學(xué)生,求抽到女生人數(shù)
名學(xué)生,求抽到女生人數(shù)![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,某鐵制零件由一個正四棱柱和一個球組成,已知正四棱柱底面邊長與球的直徑均為1cm,正四棱柱的高為2cm.現(xiàn)有這種零件一盒共50kg,取鐵的密度為![]() ,
,![]() .
.
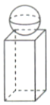
(1)估計有多少個這樣的零件;
(2)如果要給這盒零件的每個零件表面涂上一種特殊的材料,則需要能涂多少平方厘米的材料(球與棱柱接口處的面積不計,結(jié)果精確到![]() )?
)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題正確的個數(shù)是:( )
①對于兩個分類變量![]() 與
與![]() 的隨機(jī)變量
的隨機(jī)變量![]() 的觀測值
的觀測值![]() 來說,
來說,![]() 越小,判斷“
越小,判斷“![]() 與
與![]() 有關(guān)系”的把握程度越大;
有關(guān)系”的把握程度越大;
②在相關(guān)關(guān)系中,若用![]() 擬合時的相關(guān)指數(shù)為
擬合時的相關(guān)指數(shù)為![]() ,用
,用![]() 擬合時的相關(guān)指數(shù)為
擬合時的相關(guān)指數(shù)為![]() ,且
,且![]() ,則
,則![]() 的擬合效果好;
的擬合效果好;
③利用計算機(jī)產(chǎn)生![]() 之間的均勻隨機(jī)數(shù)
之間的均勻隨機(jī)數(shù)![]() ,則事件“
,則事件“![]() ”發(fā)生的概率為
”發(fā)生的概率為![]() ;
;
④“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近年空氣質(zhì)量逐步惡化,霧霾天氣現(xiàn)象出現(xiàn)增多,大氣污染危害加重.大氣污染可引起心悸、呼吸困難等心肺疾病.為了解某市心肺疾病是否與性別有關(guān),在某醫(yī)院隨機(jī)對心肺疾病入院的![]() 人進(jìn)行問卷調(diào)查,得到了如下的列聯(lián)表:
人進(jìn)行問卷調(diào)查,得到了如下的列聯(lián)表:
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 |
|
|
|
女 |
|
|
|
合計 |
|
|
|
(1)用分層抽樣的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中選
人中選![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)為了研究心肺疾病是否與性別有關(guān),請計算出統(tǒng)計量![]() ,你有多大把握認(rèn)為心肺疾病與性別有關(guān)?
,你有多大把握認(rèn)為心肺疾病與性別有關(guān)?
下面的臨界值表供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式:  ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() ,以極點為平面直角坐標(biāo)系的原點,極軸為
,以極點為平面直角坐標(biāo)系的原點,極軸為![]() 軸的正半軸,且取相等的單位長度,建立平面直角坐標(biāo)系,直線
軸的正半軸,且取相等的單位長度,建立平面直角坐標(biāo)系,直線![]() 的參數(shù)方程是
的參數(shù)方程是 (
(![]() 是參數(shù)),設(shè)點
是參數(shù)),設(shè)點![]() .
.
(Ⅰ)將曲線![]() 的極坐標(biāo)方程化為直角坐標(biāo)方程,將直線
的極坐標(biāo)方程化為直角坐標(biāo)方程,將直線![]() 的參數(shù)方程化為普通方程;
的參數(shù)方程化為普通方程;
(Ⅱ)設(shè)直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠生產(chǎn)甲,乙兩種圖畫紙,計劃每種圖畫紙的生產(chǎn)量不少于8t,已知生產(chǎn)甲種圖畫紙1t要用蘆葦7t、黃麻3t、楓樹5t;生產(chǎn)乙種圖畫紙1t要用蘆葦3t、黃麻4t、楓樹8 t.現(xiàn)在倉庫內(nèi)有蘆葦300t、黃麻150t.楓樹200t,試列出滿足題意的不等式組.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(Ⅰ)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線與坐標(biāo)軸圍成的三角形的面積;
處的切線與坐標(biāo)軸圍成的三角形的面積;
(Ⅱ)若![]() 在區(qū)間
在區(qū)間![]() 上恒成立,求實數(shù)
上恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com