www黄色av,蜜臀av粉嫩av懂色av,黄色av网址在线免费观看

精英家教網 > 高中數學 > 題目詳情

【題目】已知數列的前項和，數列的前項和，，則正整數的最大值為_________.

【答案】3

【解析】

運用數列的遞推式，結合等比數列的定義、通項公式可得an，Sn，再由數列的分組求和，結合等比數列的求和公式，以及數列的單調性，解不等式可得所求最大值．

Sn＝2﹣1，可得＝S1＝2﹣1，解得＝1；

n≥2時，＝Sn﹣Sn﹣1＝2﹣1﹣2 +1，

則＝2，可得為首項為1，公比為2的等比數列，

可得＝2n﹣1，Sn＝2n﹣1，

Sn1＝2n﹣1+（）n﹣1+1＝2n+（）n﹣1，

Tn＝（2+4+…+2n）+（1（）n﹣1）

2n+1﹣（）n﹣1，

可得Tn是一個增函數（增函數+增函數=增函數），隨著n的增大而增大，T3，

由，可得n≤3，即n的最大值為3．

故答案為：3．

練習冊系列答案

仁愛英語同步閱讀與完形填空周周練系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】某市一次全市高中男生身高統計調查數據顯示：全市100000名男生的身高服從正態分布N(168,16)．現從某學校高三年級男生中隨機抽取50名測量身高，測量發現被測學生身高全部介于160 cm和184 cm之間，將測量結果按如下方式分成6組：第1組[160,164)，第2組[164,168)，…，第6組[180,184]，如圖是按上述分組方法得到的頻率分布直方圖．

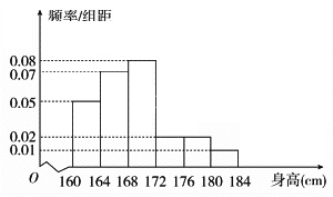
(1)由頻率分布直方圖估計該校高三年級男生平均身高狀況；

(2)求這50名男生身高在172 cm以上(含172 cm)的人數；

(3)在這50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人，將該2人中身高排名(從高到低)在全市前130名的人數記為ξ，求ξ的數學期望．

參考數據：若ξ～N(μ，σ2)，則P(μ－σ<ξ≤μ＋σ)＝0.6826，P(μ－2σ<ξ≤μ＋2σ)＝0.9544，P(μ－3σ<ξ≤μ＋3σ)＝0.9974.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】在梯形中(圖1)，，，，過、分別作的垂線，垂足分別為、，且，將梯形沿、同側折起，使得，且，得空間幾何體 (圖2).直線與平面所成角的正切值是.

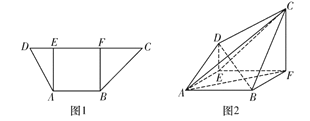
（1）求證：平面；

（2）求多面體的體積.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某校學生社團組織活動豐富，學生會為了解同學對社團活動的滿意程度，隨機選取了100位同學進行問卷調查，并將問卷中的這100人根據其滿意度評分值（百分制）按照[40，50），[50，60），[60，70），…，[90，100]分成6組，制成如圖所示頻率分布直方圖．

（1）求圖中x的值；

（2）求這組數據的中位數；

（3）現從被調查的問卷滿意度評分值在[60，80）的學生中按分層抽樣的方法抽取5人進行座談了解，再從這5人中隨機抽取2人作主題發言，求抽取的2人恰在同一組的概率．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】假設A型進口車關稅稅率在2002年是100%，在2007年是25%，2002年A型進口車每輛價格為64萬元（其中含32萬元關稅稅款）

（1）已知與A型車性能相近的B型國產車，2002年每輛價格為46萬元，若A型車的價格只受關稅降低的影響，為了保證2007年B型車的價格不高于A型車價格的90%，B型車價格要逐年減低，問平均每年至少下降多少萬元？

（2）某人在2002年將33萬元存入銀行，假設銀行扣利息稅后的年利率為1.8%（5年內不變），且每年按復利計算（上一年的利息計入第二年的本金），那么5年到期時這筆錢連本帶息是否一定夠買按（1）中所述降價后的B型車一輛？

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某公司研發了兩種具有自主知識產權的操作系統，分別命名為“天下”、“東方”.這兩套操作系統均適用于手機、電腦、車聯網、物聯網等，且較國際同類操作系統更加流暢.

（1）為了解喜歡“天下”系統是否與性別有關，隨機調查了名男用戶和名女用戶，每位用戶對“天下”系統給出喜歡或不喜歡的評價，得到下面列聯表：

請問：能否有的把握認為男、女用戶對“天下”系統的喜歡有差異？

附：.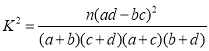

（2）該公司選定萬名用戶對“天下”和“東方”操作系統（以下簡稱“天下”、“東方”）進行測試，每個用戶只能從“天下”或“東方”中選擇一個使用，每經過一個月后就給用戶一次重新選擇“天下”或“東方”的機會.這個月選擇“天下”的用戶在下個月選擇“天下”的概率均為，選擇“東方”的概率均為，；這個月選擇“東方”的用戶在下個月選擇“天下”的概率均為，選擇“東方”的概率均為，.記表示第個月用戶選擇“天下”的概率，已知，，，，.