
【題目】某市一次全市高中男生身高統計調查數據顯示:全市100000名男生的身高服從正態分布N(168,16).現從某學校高三年級男生中隨機抽取50名測量身高,測量發現被測學生身高全部介于160 cm和184 cm之間,將測量結果按如下方式分成6組:第1組[160,164),第2組[164,168),…,第6組[180,184],如圖是按上述分組方法得到的頻率分布直方圖.
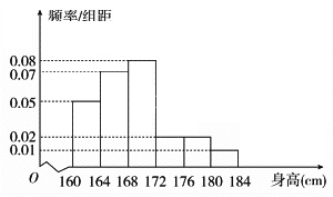
(1)由頻率分布直方圖估計該校高三年級男生平均身高狀況;
(2)求這50名男生身高在172 cm以上(含172 cm)的人數;
(3)在這50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,將該2人中身高排名(從高到低)在全市前130名的人數記為ξ,求ξ的數學期望.
參考數據:若ξ~N(μ,σ2),則P(μ-σ<ξ≤μ+σ)=0.6826,P(μ-2σ<ξ≤μ+2σ)=0.9544,P(μ-3σ<ξ≤μ+3σ)=0.9974.
【答案】(Ⅰ)高于全市的平均值168。
(Ⅱ)這50名男生身高在172 cm以上(含172 cm)的人數為10人.
(Ⅲ)![]()
【解析】
試題(Ⅰ)由直方圖,經過計算該校高三年級男生平均身高為
![]() ,
,
高于全市的平均值168(或者:經過計算該校高三年級男生平均身高為168.72,比較接近全市的平均值168). …………………………………………………………(4分)
(Ⅱ)由頻率分布直方圖知,后三組頻率為(0.02+0.02+0.01)×4=0.2,人數為0.2×5=10,即這50名男生身高在172 cm以上(含172 cm)的人數為10人. ……………(6分)
(Ⅲ)![]()
![]() ,
,
![]() ,0.0013×100 000=130.
,0.0013×100 000=130.
所以,全市前130名的身高在180 cm以上,這50人中180 cm以上的有2人.
隨機變量![]() 可取
可取![]() ,于是
,于是
![]() ,
,![]() ,
,![]()
![]() . …………………(12分)
. …………………(12分)


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知點F為拋物線![]() 的焦點,過點F的動直線l與拋物線C交于M,N兩點,且當直線l的傾斜角為
的焦點,過點F的動直線l與拋物線C交于M,N兩點,且當直線l的傾斜角為![]() 時,
時,![]() .
.
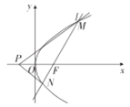
(1)求拋物線C的方程.
(2)點![]() ,證明:直線PM,PN關于x軸對稱.
,證明:直線PM,PN關于x軸對稱.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 過點
過點![]() ,焦點
,焦點![]() ,圓
,圓![]() 的直徑為
的直徑為![]() .
.
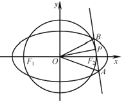
(1)求橢圓![]() 及圓
及圓![]() 的方程;
的方程;
(2)設直線![]() 與圓
與圓![]() 相切于第一象限內的點
相切于第一象限內的點![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點.若
兩點.若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() (
(![]() 為常數,
為常數,![]() ,
,![]() ,
,![]() ),給出下列四個結論:①若數列
),給出下列四個結論:①若數列![]() 是周期數列,則周期必為2:②若
是周期數列,則周期必為2:②若![]() ,則數列
,則數列![]() 必是常數列:③若
必是常數列:③若![]() ,則數列
,則數列![]() 是遞增數列:④若
是遞增數列:④若![]() ,則數列
,則數列![]() 是有窮數列,其中,所有錯誤結論的序號是________.
是有窮數列,其中,所有錯誤結論的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() (
(![]() )的上頂點為
)的上頂點為![]() ,圓
,圓![]() 經過點
經過點![]() .
.
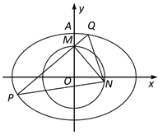
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作直線
作直線![]() 的垂線
的垂線![]() 交圓
交圓![]() 于另一點
于另一點![]() .若△PQN的面積為3,求直線
.若△PQN的面積為3,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“搜索指數”是網民通過搜索引擎,以每天搜索關鍵詞的次數為基礎所得到的統計指標.“搜索指數”越大,表示網民對該關鍵詞的搜索次數越多,對該關鍵詞相關的信息關注度也越高.下圖是2017年9月到2018年2月這半年中,某個關鍵詞的搜索指數變化的走勢圖.

根據該走勢圖,下列結論正確的是( )
A. 這半年中,網民對該關鍵詞相關的信息關注度呈周期性變化
B. 這半年中,網民對該關鍵詞相關的信息關注度不斷減弱
C. 從網民對該關鍵詞的搜索指數來看,去年10月份的方差小于11月份的方差
D. 從網民對該關鍵詞的搜索指數來看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟的發展,個人收入的提高,自2019年1月1日起,個人所得稅起征點和稅率的調整.調整如下:納稅人的工資、薪金所得,以每月全部收入額減除5000元后的余額為應納稅所得額.依照個人所得稅稅率表,調整前后的計算方法如下表:
個人所得稅稅率表(調整前) | 個人所得稅稅率表(調整后) | ||||
免征額3500元 | 免征額5000元 | ||||
級數 | 全月應納稅所得額 | 稅率( | 級數 | 全月應納稅所得額 | 稅率( |
1 | 不超過1500元部分 | 3 | 1 | 不超過3000元部分 | 3 |
2 | 超過1500元至4500元的部分 | 10 | 2 | 超過3000元至12000元的部分 | 10 |
3 | 超過4500元至9000元的部分 | 20 | 3 | 超過12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
(1)假如小紅某月的工資、薪金等所得稅前收入總和不高于8000元,記![]() 表示總收入,
表示總收入,![]() 表示應納的稅,試寫出調整前后
表示應納的稅,試寫出調整前后![]() 關于
關于![]() 的函數表達式;
的函數表達式;
(2)某稅務部門在小紅所在公司利用分層抽樣方法抽取某月100個不同層次員工的稅前收入,并制成下面的頻數分布表:
收入 (元) |
|
|
|
|
|
|
人數 | 30 | 40 | 10 | 8 | 7 | 5 |
先從收入在![]() 及
及![]() 的人群中按分層抽樣抽取7人,再從中選2人作為新納稅法知識宣講員,求兩個宣講員不全是同一收入人群的概率;
的人群中按分層抽樣抽取7人,再從中選2人作為新納稅法知識宣講員,求兩個宣講員不全是同一收入人群的概率;
(3)小紅該月的工資、薪金等稅前收入為7500元時,請你幫小紅算一下調整后小紅的實際收入比調整前增加了多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com