
【題目】在直角坐標系內,點![]() 實施變換
實施變換![]() 后,對應點為
后,對應點為![]() ,給出以下命題:
,給出以下命題:
①圓![]() 上任意一點實施變換
上任意一點實施變換![]() 后,對應點的軌跡仍是圓
后,對應點的軌跡仍是圓![]() ;
;
②若直線![]() 上每一點實施變換
上每一點實施變換![]() 后,對應點的軌跡方程仍是
后,對應點的軌跡方程仍是![]() 則
則![]() ;
;
③橢圓![]() 上每一點實施變換
上每一點實施變換![]() 后,對應點的軌跡仍是離心率不變的橢圓;
后,對應點的軌跡仍是離心率不變的橢圓;
④曲線![]() 上每一點實施變換
上每一點實施變換![]() 后,對應點的軌跡是曲線
后,對應點的軌跡是曲線![]() ,
,![]() 是曲線
是曲線![]() 上的任意一點,
上的任意一點,![]() 是曲線
是曲線![]() 上的任意一點,則
上的任意一點,則![]() 的最小值為
的最小值為![]() .
.
以上正確命題的序號是___________________(寫出全部正確命題的序號).
【答案】①③④
【解析】
利用點![]() 實施變換
實施變換![]() 后,對應點為
后,對應點為![]() 這一變換過程,針對每一個方程給出變換后的正確方程,從而可得結果.
這一變換過程,針對每一個方程給出變換后的正確方程,從而可得結果.
①圓![]() 上任意一點實施變換
上任意一點實施變換![]() 后,
后,
顯然互換![]() 后,對應點的軌跡仍是圓
后,對應點的軌跡仍是圓![]() ,故①正確;
,故①正確;
②直線![]() 上每一點實施變換
上每一點實施變換![]() 后,互換
后,互換![]() 后,對應點的軌跡方程
后,對應點的軌跡方程![]() ,若應點的軌跡仍是
,若應點的軌跡仍是![]() ,那么
,那么![]() 且
且![]() ,故②錯誤;
,故②錯誤;
③橢圓![]() 上每一點實施變換
上每一點實施變換![]() 后,對應點的軌跡
后,對應點的軌跡![]() ,兩個橢圓的離心率相等,所以對應點的軌跡仍是離心率不變的橢圓,故③正確;
,兩個橢圓的離心率相等,所以對應點的軌跡仍是離心率不變的橢圓,故③正確;
④曲線![]() 上每一點實施變換
上每一點實施變換![]() 后,
后,
對應點的軌跡是![]() ,
,
則曲線![]() 與曲線
與曲線![]() 關于
關于![]() 對稱,
對稱,
設與![]() 平行且分別與曲線
平行且分別與曲線![]() 與曲線
與曲線![]() 相切的直線方程分別為
相切的直線方程分別為
![]() 與
與![]() ,根據判別式為零可得
,根據判別式為零可得
與![]() 平行且分別與曲線
平行且分別與曲線![]() 與曲線
與曲線![]() 相切是直線方程為
相切是直線方程為![]() 和
和![]() ,
,
![]() 的最小值就是直線
的最小值就是直線![]() 與
與![]() 的距離為
的距離為![]() ,
,
所以,故④正確,故答案為①③④.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以原點
),以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 是曲線
是曲線![]() 上一點,若點
上一點,若點![]() 到曲線
到曲線![]() 的最小距離為
的最小距離為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某二手交易市場對某型號的二手汽車的使用年數![]() (
(![]() )與銷售價格
)與銷售價格![]() (單位:萬元/輛)進行整理,得到如下的對應數據:
(單位:萬元/輛)進行整理,得到如下的對應數據:
使用年數 | 2 | 4 | 6 | 8 | 10 |
銷售價格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)試求![]() 關于
關于![]() 的回歸直線方程
的回歸直線方程![]() .
.
(參考公式: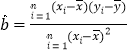 ,
,![]() )
)
(II)已知每輛該型號汽車的收購價格為![]() 萬元,根據(I)中所求的回歸方程,預測
萬元,根據(I)中所求的回歸方程,預測![]() 為何值時,銷售一輛該型號汽車所獲得的利潤
為何值時,銷售一輛該型號汽車所獲得的利潤![]() 最大?(利潤=銷售價格-收購價格)
最大?(利潤=銷售價格-收購價格)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了了解學生每天平均課外閱讀的時間(單位:分鐘),從本校隨機抽取了100名學生進行調查,根據收集的數據,得到學生每天課外閱讀時間的頻率分布直方圖,如圖所示,若每天課外閱讀時間不超過30分鐘的有45人.
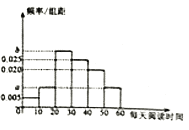
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)根據頻率分布直方圖,估計該校學生每天課外閱讀時間的中位數及平均值(同一組中的數據用該組區間的中點值代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設D是函數y=f(x)定義域內的一個區間,若存在x0∈D,使f(x0)=﹣x0 , 則稱x0是f(x)的一個“次不動點”,也稱f(x)在區間D上存在次不動點.若函數f(x)=ax2﹣3x﹣a+ ![]() 在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
A.(﹣∞,0)
B.(0, ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題a2x2+ax﹣2=0在[﹣1,1]上有解;命題q:只有一個實數x滿足不等式x2+2ax+2a≤0,若命題“p”或“q”是假命題,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市隨機抽取一年(365天)內100天的空氣質量指數API的監測數據,結果統計如下:
API | [0,100] | (100,200] | (200,300] | >300 |
空氣質量 | 優良 | 輕污染 | 中度污染 | 重度污染 |
天數 | 17 | 45 | 18 | 20 |
記某企業每天由空氣污染造成的經濟損失S(單位:元),空氣質量指數API為![]() .當
.當![]() 時,企業沒有造成經濟損失;當
時,企業沒有造成經濟損失;當![]() 對企業造成經濟損失成直線模型(當
對企業造成經濟損失成直線模型(當![]() 時造成的經濟損失為
時造成的經濟損失為![]() ,當
,當![]() 時,造成的經濟損失
時,造成的經濟損失![]() );當
);當![]() 時造成的經濟損失為2000元;
時造成的經濟損失為2000元;
(1)試寫出![]() 的表達式;
的表達式;
(2)若本次抽取的樣本數據有30天是在供暖季,其中有12天為重度污染,完成下面2×2列聯表,并判斷能否有99%的把握認為該市本年空氣重度污染與供暖有關?
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
![]()
P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正四棱柱ABCD﹣A1B1C1D1(底面是正方形,側棱垂直于底面)的8個頂點都在球O的表面上,AB=1,AA1′=2,則球O的半徑R=;若E,F是棱AA1和DD1的中點,則直線EF被球O截得的線段長為 . 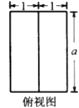
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com