
【題目】如圖,在平面直角坐標系xOy中,橢圓E: ![]() =1(a>b>0)的左頂點為A(﹣2,0),離心率為
=1(a>b>0)的左頂點為A(﹣2,0),離心率為 ![]() ,過點A的直線l與橢圓E交于另一點B,點C為y軸上的一點.
,過點A的直線l與橢圓E交于另一點B,點C為y軸上的一點.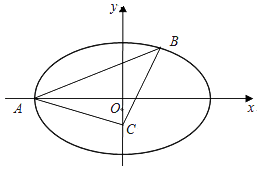
(1)求橢圓E的標準方程;
(2)若△ABC是以點C為直角頂點的等腰直角三角形,求直線l的方程.
【答案】
(1)解:由題意可得:  ,從而有b2=a2﹣c2=3,
,從而有b2=a2﹣c2=3,
所以橢圓E的標準方程為: ![]()
(2)解:設直線l的方程為y=k(x+2),代入為: ![]() ,
,
得(3+4k2)x2+16k2x+16k2﹣12=0
因為x=﹣2為該方程的一個根,解得B( ![]() ,
, ![]() ),
),
設C(x0,y0),由kACkBC=﹣1,得: 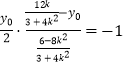 ,
,
即:(3+4k2)y02﹣12ky0+(16k2﹣12)=0 ①
由AC=BC,即AC2=BC2,得4+y02=( ![]() )2+(y0﹣
)2+(y0﹣ ![]() )2,
)2,
即4= ![]() +(
+( ![]() )2﹣
)2﹣ ![]() ,
,
即4(3+4k2)2=(6﹣8k2)2+144k2﹣24(3+4k2)y0…①,
所以k=0或y0= ![]() ,
,
當k=0時,直線l的方程為y=0,
當y0= ![]() 時,代入①得16k4+7k2﹣9=0,解得k=
時,代入①得16k4+7k2﹣9=0,解得k= ![]() ,
,
此時直線l的方程為y=± ![]() (x+2)
(x+2)
綜上,直線l的方程為y=0,y=± ![]() (x+2)
(x+2)
【解析】(1)根據橢圓的特性可得a、b的值進而得到橢圓的方程。(2)聯立橢圓和直線的方程,點A在橢圓上,解得點B的坐標,利用設而不求法設出點C
的坐標,根據兩條直線垂直斜率值即為-1得到關于x0、y0的一個方程,根據AC=BC得到另一個關于x0、y0的方程,聯立兩式解得k和y0的值,分情況討論
當k=0時,直線l的方程為y=0,當![]() 時,求出k= ±
時,求出k= ± ![]() ,進而得到直線的方程。
,進而得到直線的方程。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x2﹣x﹣1)ex .
(1)求函數f(x)的單調區間.
(2)若方程a( ![]() +1)+ex=ex在(0,1)內有解,求實數a的取值范圍.
+1)+ex=ex在(0,1)內有解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知總體的各個體的值由小到大依次為2,3,3,7,a,b,12,13.7,18.3,20,且總體的中位數為10.5,平均數為10.若要使該總體的方差最小,則a、b的取值分別是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記函數f(x)=lg(1﹣ax2)的定義域、值域分別為集合A,B.
(1)當a=1時,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學在上學路上要經過A、B、C三個帶有紅綠燈的路口.已知他在A、B、C三個路口遇到紅燈的概率依次是 ![]() 、
、 ![]() 、
、 ![]() ,遇到紅燈時停留的時間依次是40秒、20秒、80秒,且在各路口是否遇到紅燈是相互獨立的.
,遇到紅燈時停留的時間依次是40秒、20秒、80秒,且在各路口是否遇到紅燈是相互獨立的.
(1)求這名同學在上學路上在第三個路口首次遇到紅燈的概率;,
(2)求這名同學在上學路上因遇到紅燈停留的總時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若實數x,y滿足的約束條件 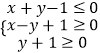 ,將一顆骰子投擲兩次得到的點數分別為a,b,則函數z=2ax+by在點(2,﹣1)處取得最大值的概率為( )
,將一顆骰子投擲兩次得到的點數分別為a,b,則函數z=2ax+by在點(2,﹣1)處取得最大值的概率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com