
【題目】已知橢圓C:mx2+3my2=1(m>0)的長軸長為 ![]() ,O為坐標原點.
,O為坐標原點.
(1)求橢圓C的方程和離心率.
(2)設點A(3,0),動點B在y軸上,動點P在橢圓C上,且點P在y軸的右側.若BA=BP,求四邊形OPAB面積的最小值.
【答案】
(1)
解:由題意知橢圓C: ![]() ,
,
所以 ![]() ,
, ![]() ,
,
故 ![]() ,解得
,解得 ![]() ,
,
所以橢圓C的方程為 ![]() .
.
因為 ![]() ,所以離心率
,所以離心率 ![]()
(2)
解:設線段AP的中點為D.
因為BA=BP,所以BD⊥AP.
由題意知直線BD的斜率存在,
設點P的坐標為(x0,y0)(y0≠0),
則點D的坐標為 ![]() ,直線AP的斜率
,直線AP的斜率 ![]() ,
,
所以直線BD的斜率 ![]() ,
,
故直線BD的方程為 ![]() .
.
令x=0,得 ![]() ,故
,故 ![]() .
.
由 ![]() ,得
,得 ![]() ,化簡得
,化簡得 ![]() .
.
因此,S四邊形OPAB=S△OAP+S△OAB= ![]()
= ![]() =
= ![]() =
= ![]() .
.
當且僅當 ![]() 時,即
時,即 ![]() 時等號成立.
時等號成立.
故四邊形OPAB面積的最小值為 ![]()
【解析】(1)將橢圓方程化為標準方程,由題意可得a,可得b,即可得到橢圓方程,再由離心率公式計算即可得到所求值;(2)設AP中點為D,由|BA|=||BP|,所以BD⊥AP,求得AP的斜率,進而得到BD的斜率和中點,可得直線BD的方程,即有B的坐標,求得四邊形OPAB的面積為S=S△OAP+S△OMB , 化簡整理,運用基本不等式即可得到最小值.
【考點精析】根據題目的已知條件,利用橢圓的標準方程的相關知識可以得到問題的答案,需要掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】選修4-5:不等式選講
已知不等式|x+3|﹣2x﹣1<0的解集為(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函數f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零點,求實數m的值.
|﹣x0(m>0)有零點,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M過C(1,-1),D(-1,1)兩點,且圓心M在x+y-2=0上.
(1)求圓M的方程;
(2)設點P是直線3x+4y+8=0上的動點,PA,PB是圓M的兩條切線,A,B為切點,求四邊形PAMB面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓C:![]() 的離心率為
的離心率為![]() ,其右焦點到橢圓C外一點
,其右焦點到橢圓C外一點![]() 的距離為
的距離為![]() ,不過原點O的直線l與橢圓C相交于A,B兩點,且線段AB的長度為2.
,不過原點O的直線l與橢圓C相交于A,B兩點,且線段AB的長度為2.
![]() 1
1![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 2
2![]() 求
求![]() 面積S的最大值.
面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中是錯誤命題的個數有( )
(1)若命題p為假命題,命題![]() 為假命題,則命題“
為假命題,則命題“![]() ”為假命題;
”為假命題;
(2)命題“若![]() ,則
,則![]() 或
或![]() ”的否命題為“若
”的否命題為“若![]() ,則
,則![]() 或
或![]() ”;
”;
(3)對立事件一定是互斥事件;
(4)![]() 為兩個事件,則P(A∪B)=P(A)+P(B);
為兩個事件,則P(A∪B)=P(A)+P(B);
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 通項公式為 ![]() .
.
(Ⅰ)計算f(1),f(2),f(3)的值;
(Ⅱ)比較f(n)與1的大小,并用數學歸納法證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下莖葉圖記錄了甲、乙兩組各四名同學的植樹棵數。乙組記錄中有一個數據模糊,無法確認,在圖中經X表示。
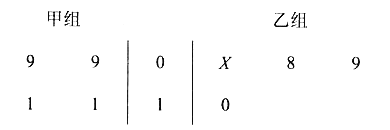
(1)如果X=8,求乙組同學植樹棵數的平均數和方差
(2)如果X=9,分別從甲、乙兩組中隨機選取一名同學,求這兩名同學的植樹總棵數為19的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的圓心坐標![]() 且與線y=3x+4相切,
且與線y=3x+4相切,
(1)求圓C的方程;
(2)設直線![]() 與圓C交于M,N兩點,那么以MN為直徑的圓能否經過原點,若能,請求出直線MN的方程;若不能,請說明理由.
與圓C交于M,N兩點,那么以MN為直徑的圓能否經過原點,若能,請求出直線MN的方程;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com