【題目】在線段
的兩端點各置一個光源，已知光源
，
的發光強度之比為
，則線段上光照度最小的一點到，的距離之比為______（光學定律：
點的光照度與到光源的距離的平方成反比，與光源的發光強度成正比）
【答案】
【解析】
設線段長為L，線段上光照度最小的一點P到
，
的距離分別為
，不妨設，光源的發光強度之比為1，2，由題意可得P點受光源的照度為：
，P點受光源的照度為：
，作和后利用導數求最值，可得P到，的距離，作比得答案．
解：設線段長為L，線段上光照度最小的一點P到，的距離分別為，不妨設，光源的發光強度為1，2，
∵光照度與光的強度成正比，設比例系數為
，
與光源距離的平方成反比，設比例系數為
，
故P點受光源的照度為：，
P點受光源的照度為：，
故P點受到，兩光源的總照度
，
，
令
，解得：
，
當
時，
，函數
在
上遞減，
當
時，
，函數在
上遞增，
故當時，
取極小值，且是最小值，
故P在線段上距離為
時，P點的光照度最小，
此時點P到的距離，之比為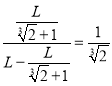
．
故答案為：.
科目：高中數學 來源： 題型：
【題目】一個口袋內裝有大小相同的5個球，其中3個白球，2個黑球，從中一次摸出兩個球．
（1）共有多少個基本事件？
（2）摸出的兩個都是白球的概率是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
，如果對于定義域
內的任意實數
，對于給定的非零常數
，總存在非零常數
，恒有
成立，則稱函數
是上的級類增周期函數，周期為，若恒有
成立，則稱函數是上的級類周期函數，周期為.
（1）已知函數
是
上的周期為1的2級類增周期函數，求實數
的取值范圍；
（2）已知
，是
上級類周期函數，且是上的單調遞增函數，當
時，
，求實數的取值范圍；
（3）是否存在實數
，使函數
是
上的周期為的級類周期函數，若存在，求出實數和的值，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△
的三個內角
、
、
所對應的邊分別為
、
、
，復數
，
，（其中
是虛數單位），且
.
（1）求證：
，并求邊長的值；
（2）判斷△的形狀，并求當
時，角的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，曲線C的參數方程是
（
為參數），把曲線C的橫坐標縮短為原來的
，縱坐標縮短為原來的一半，得到曲線
直線l的普通方程是
，以坐標原點O為極點，x軸正半軸為極軸建立極坐標系.
（1）求直線l的極坐標方程和曲線的普通方程；
（2）記射線
（
）與交于點A，與l交于點B，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
的在數集
上都有定義，對于任意的
，當
時，
或
成立，則稱是數集上的限制函數.
（1）求
在
上的限制函數的解析式；
（2）證明：如果在區間
上恒為正值，則在
上是增函數；[注：如果在區間上恒為負值，則在區間上是減函數，此結論無需證明，可以直接應用]
（3）利用（2）的結論，求函數
在
上的單調區間.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為F,直線
與
軸的交點為P,與C的交點為Q,且
過F的直線
與C相交于A、B兩點.
(1)求C的方程；
(2)設點
且
的面積為
求直線的方程；
(3)若線段AB的垂直平分線與C相交于M、N兩點,且A、M、B、N四點在同一圓上,求直線的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
