
【題目】已知拋物線![]() 的焦點為F,直線
的焦點為F,直線![]() 與
與![]() 軸的交點為P,與C的交點為Q,且
軸的交點為P,與C的交點為Q,且![]() 過F的直線
過F的直線![]() 與C相交于A、B兩點.
與C相交于A、B兩點.
(1)求C的方程;
(2)設點![]() 且
且![]() 的面積為
的面積為![]() 求直線
求直線![]() 的方程;
的方程;
(3)若線段AB的垂直平分線與C相交于M、N兩點,且A、M、B、N四點在同一圓上,求直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,或
,或![]()
【解析】
(1)設點![]() 的坐標為
的坐標為![]() ,把點
,把點![]() 的坐標代入拋物線
的坐標代入拋物線![]() 的方程,求得
的方程,求得![]() ,根據
,根據![]() 求得
求得![]() 的值,可得
的值,可得![]() 的方程;
的方程;
(2)設![]() 的方程為
的方程為![]() ,代入拋物線方程化簡,利用韋達定理、弦長公式求得弦長
,代入拋物線方程化簡,利用韋達定理、弦長公式求得弦長![]() ,再求出點
,再求出點![]() 到直線
到直線![]() 的距離,利用
的距離,利用![]() 的面積列方程求解即可;
的面積列方程求解即可;
(3)把直線MN的方程代入拋物線方程化簡,利用韋達定理、弦長公式求得![]() .由于MN垂直平分線段AB,若MN的中點為H,故AMBN四點共圓等價于
.由于MN垂直平分線段AB,若MN的中點為H,故AMBN四點共圓等價于![]() ,由此求得m的值,可得直線
,由此求得m的值,可得直線![]() 的方程.
的方程.
解:(1)設點![]() 的坐標為
的坐標為![]() ,把點
,把點![]() 的坐標代入拋物線
的坐標代入拋物線![]() ,
,
可得![]() ,
,
![]() 點
點![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,求得
,求得![]() ,或
,或![]() (舍去)。
(舍去)。
故C的方程為![]() .
.
(2)由題意可得,直線![]() 和坐標軸不垂直,
和坐標軸不垂直,![]() 的焦點為
的焦點為![]() ,
,
設![]() 的方程為
的方程為![]() ,代入拋物線方程得
,代入拋物線方程得
![]() ,
,
顯然判別式![]() ,
,
![]() AB的中點坐標
AB的中點坐標![]() 。
。
弦長![]()
![]() 的方程為
的方程為![]() ,即
,即![]() ,
,
![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
![]()
解得![]() ,
,
故直線![]() 的方程為
的方程為![]() 或
或![]()
(3)因為線段AB的垂直平分線與C相交于M、N兩點,
設直線MN的方程為![]() ,
,
把線MN的方程代入拋物線方程可得![]() ,
,
![]() ,
,
故線段MN的中點H的坐標為![]() ,
,
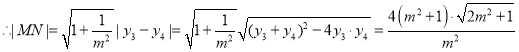 ,
,
∵MN垂直平分線段AB,故AMBN四點共圓等價于![]() ,
,
![]() ,
,
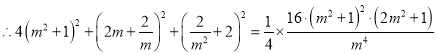
化簡可得![]() ,
,
![]() ,
,
∴直線![]() 的方程為
的方程為![]() ,或
,或![]() .
.


科目:高中數學 來源: 題型:
【題目】在線段![]() 的兩端點各置一個光源,已知光源
的兩端點各置一個光源,已知光源![]() ,
,![]() 的發光強度之比為
的發光強度之比為![]() ,則線段上光照度最小的一點到
,則線段上光照度最小的一點到![]() ,
,![]() 的距離之比為______(光學定律:
的距離之比為______(光學定律:![]() 點的光照度與
點的光照度與![]() 到光源的距離的平方成反比,與光源的發光強度成正比)
到光源的距離的平方成反比,與光源的發光強度成正比)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有10名選手參加某項詩詞比賽,計分規則如下:比賽共有6道題,對于每一道題,10名選手都必須作答,若恰有![]() 個人答錯,則答對的選手該題每人得
個人答錯,則答對的選手該題每人得![]() 分,答錯選手該題不得分.比賽結束后,關于選手得分情況有如下結論:
分,答錯選手該題不得分.比賽結束后,關于選手得分情況有如下結論:
①若選手甲答對6道題,選手乙答對5道題,則甲比乙至少多得1分:
②若選手甲和選手乙都答對5道題,則甲和乙得分相同;
③若選手甲的總分比其他選手都高,則甲最高可得54分
其中正確結論的個數是( )
A.0B.3C.2D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 某創業投資公司擬投資開發某種新能源產品,估計能獲得25萬元~ 1600萬元的投資收益,現準備制定一個對科研課題組的獎勵方案:獎金y(單位:萬元)隨投資收益x(單位:萬元)的增加而增加,獎金不超過75萬元,同時獎金不超過投資收益的20%.(即:設獎勵方案函數模型為y=f (x)時,則公司對函數模型的基本要求是:當x∈[25,1600]時,①f(x)是增函數;②f (x) ![]() 75恒成立;
75恒成立; ![]()
![]() 恒成立.
恒成立.
(1)判斷函數![]() 是否符合公司獎勵方案函數模型的要求,并說明理由;
是否符合公司獎勵方案函數模型的要求,并說明理由;
(2)已知函數![]() 符合公司獎勵方案函數模型要求,求實數a的取值范圍.
符合公司獎勵方案函數模型要求,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公園內有一塊以O為圓心半徑為20米的圓形區域.為豐富市民的業余文化生活,現提出如下設計方案:如圖,在圓形區域內搭建露天舞臺,舞臺為扇形OAB區域,其中兩個端點A,B分別在圓周上;觀眾席為等腰梯形ABQP內且在圓O外的區域,其中![]() ,
,![]() ,且AB,PQ在點O的同側.為保證視聽效果,要求觀眾席內每一個觀眾到舞臺中心O處的距離都不超過60米(即要求
,且AB,PQ在點O的同側.為保證視聽效果,要求觀眾席內每一個觀眾到舞臺中心O處的距離都不超過60米(即要求![]() ).設
).設![]() ,
,![]() .
.
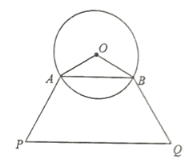
(1)當![]() 時求舞臺表演區域的面積;
時求舞臺表演區域的面積;
(2)對于任意α,上述設計方案是否均能符合要求?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為圓
為圓![]() 的圓心,
的圓心, ![]() 是圓上的動點,點
是圓上的動點,點![]() 在圓的半徑
在圓的半徑![]() 上,且有點
上,且有點![]() 和
和![]() 上的點
上的點![]() ,滿足
,滿足![]() ,
, ![]() .
.
(1)當點![]() 在圓上運動時,求點
在圓上運動時,求點![]() 的軌跡方程;
的軌跡方程;
(2)若斜率為![]() 的直線
的直線![]() 與圓
與圓![]() 相切,直線
相切,直線![]() 與(1)中所求點
與(1)中所求點![]() 的軌跡交于不同的兩點
的軌跡交于不同的兩點![]() ,
, ![]() ,
, ![]() 是坐標原點,且
是坐標原點,且![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一顆質地均勻的正方體骰子(六個面的點數分別為1、2、3、4、5、6)先后拋擲兩次,記第一次出現的點數為![]() ,第二次出現的點數為
,第二次出現的點數為![]() .
.
(1)設復數![]() (
(![]() 為虛數單位),求事件“
為虛數單位),求事件“![]() 為實數”的概率;
為實數”的概率;
(2)求點![]() 落在不等式組
落在不等式組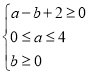 表示的平面區域內(含邊界)的概率.
表示的平面區域內(含邊界)的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com