
【題目】設(shè)函數(shù)f(x)=aexlnx+ ![]() ,曲線y=f(x)在點(1,f(1))處得切線方程為y=e(x﹣1)+2.
,曲線y=f(x)在點(1,f(1))處得切線方程為y=e(x﹣1)+2.
(Ⅰ)求a、b;
(Ⅱ)證明:f(x)>1.
【答案】解:(Ⅰ)函數(shù)f(x)的定義域為(0,+∞),f′(x)= ![]() +
+ ![]() ,
,
由題意可得f(1)=2,f′(1)=e,
故a=1,b=2;
(Ⅱ)由(Ⅰ)知,f(x)=exlnx+ ![]() ,
,
∵f(x)>1,∴exlnx+ ![]() >1,∴l(xiāng)nx>
>1,∴l(xiāng)nx> ![]() ﹣
﹣ ![]() ,
,
∴f(x)>1等價于xlnx>xe﹣x﹣ ![]() ,設(shè)函數(shù)g(x)=xlnx,則g′(x)=1+lnx,
,設(shè)函數(shù)g(x)=xlnx,則g′(x)=1+lnx,
∴當x∈(0, ![]() )時,g′(x)<0;當x∈(
)時,g′(x)<0;當x∈( ![]() ,+∞)時,g′(x)>0.
,+∞)時,g′(x)>0.
故g(x)在(0, ![]() )上單調(diào)遞減,在(
)上單調(diào)遞減,在( ![]() ,+∞)上單調(diào)遞增,從而g(x)在(0,+∞)上的最小值為g(
,+∞)上單調(diào)遞增,從而g(x)在(0,+∞)上的最小值為g( ![]() )=﹣
)=﹣ ![]() .
.
設(shè)函數(shù)h(x)=xe﹣x﹣ ![]() ,則h′(x)=e﹣x(1﹣x).
,則h′(x)=e﹣x(1﹣x).
∴當x∈(0,1)時,h′(x)>0;當x∈(1,+∞)時,h′(x)<0,
故h(x)在(0,1)上單調(diào)遞增,在(1,+∞)上單調(diào)遞減,
從而h(x)在(0,+∞)上的最大值為h(1)=﹣ ![]() .
.
綜上,當x>0時,g(x)>h(x),即f(x)>1
【解析】(Ⅰ)求出定義域,導數(shù)f′(x),根據(jù)題意有f(1)=2,f′(1)=e,解出即可;(Ⅱ)由(Ⅰ)知,f(x)>1等價于xlnx>xe﹣x﹣ ![]() ,設(shè)函數(shù)g(x)=xlnx,函數(shù)h(x)=
,設(shè)函數(shù)g(x)=xlnx,函數(shù)h(x)= ![]() ,只需證明g(x)min>h(x)max , 利用導數(shù)可分別求得g(x)min , h(x)max;
,只需證明g(x)min>h(x)max , 利用導數(shù)可分別求得g(x)min , h(x)max;


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
已知過點![]() 的直線
的直線![]() 的參數(shù)方程是
的參數(shù)方程是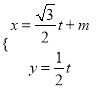 (
(![]() 為參數(shù)).以平面直角坐標系的原點為極點,
為參數(shù)).以平面直角坐標系的原點為極點, ![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程式為
的極坐標方程式為![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,且
,且![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=|x2﹣1|+x2﹣kx.
(1)若k=2時,求出函數(shù)f(x)的單調(diào)區(qū)間及最小值;
(2)若f(x)≥0恒成立,求實數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為提高信息在傳輸中的抗干擾能力,通常在原信息中按一定規(guī)則加入相關(guān)數(shù)據(jù)組成傳輸信息.設(shè)定原信息為![]()
![]() (
(![]() ),傳輸信息為
),傳輸信息為![]() ,其中
,其中![]() ,
,![]() 運算規(guī)則為:
運算規(guī)則為:![]() ,
,![]() ,
,![]() ,
,![]() ,例如原信息為111,則傳輸信息為01111.傳輸信息在傳輸過程中受到干擾可能導致接收信息出錯,則下列接收信息一定有誤的是( )
,例如原信息為111,則傳輸信息為01111.傳輸信息在傳輸過程中受到干擾可能導致接收信息出錯,則下列接收信息一定有誤的是( )
A. 11010 B. 01100 C. 10111 D. 00011
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=(x-k)ex,
(1)求f(x)的單調(diào)區(qū)間;
(2)求f(x)在區(qū)間[0,1]上的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給定函數(shù)① ![]() ,②
,② ![]() ,③y=|x﹣1|,④y=2x+1 , 其中在區(qū)間(0,1)上單調(diào)遞減的函數(shù)序號是( )
,③y=|x﹣1|,④y=2x+1 , 其中在區(qū)間(0,1)上單調(diào)遞減的函數(shù)序號是( )
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(12分)某同學參加3門課程的考試。假設(shè)該同學第一門課程取得優(yōu)秀成績的概率為![]() ,第二、第三門課程取得優(yōu)秀成績的概率分別為
,第二、第三門課程取得優(yōu)秀成績的概率分別為![]() ,
,![]() (
(![]() >
>![]() ),且不同課程是否取得優(yōu)秀成績相互獨立。記ξ為該生取得優(yōu)秀成績的課程數(shù),其分布列為
),且不同課程是否取得優(yōu)秀成績相互獨立。記ξ為該生取得優(yōu)秀成績的課程數(shù),其分布列為
ξ | 0 | 1 | 2 | 3 |
|
|
|
|
|
(Ⅰ)求該生至少有1門課程取得優(yōu)秀成績的概率;
(Ⅱ)求![]() ,
,![]() 的值;
的值;
(Ⅲ)求數(shù)學期望![]() ξ。
ξ。
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com