
【題目】(題文)如圖,在五面體ABCDEF中,四邊形EDCF是正方形,![]() .
.

(1)證明:![]() ;
;
(2)已知四邊形ABCD是等腰梯形,且![]() ,求五面體ABCDEF的體積.
,求五面體ABCDEF的體積.
【答案】(1)見解析;(2)見解析.
【解析】
分析:(1)先根據線面垂直判定定理得![]() 平面
平面![]() .,即得
.,即得![]() . 再根據平行關系得結論,(2)先分割
. 再根據平行關系得結論,(2)先分割![]() . 過
. 過![]() 作
作![]() ,根據線面垂直判定定理得
,根據線面垂直判定定理得![]() 平面
平面![]() ,則
,則![]() 是四棱錐
是四棱錐![]() 的高.由(1)可得
的高.由(1)可得![]() 平面
平面![]() ,則
,則![]() 是三棱錐
是三棱錐![]() 的高.最后根據錐體體積公式求體積.
的高.最后根據錐體體積公式求體積.
詳解:(1)證明:由已知的![]() ,
,![]() ,
,![]() 、
、![]()
![]() 平面
平面![]() ,且
,且![]() ∩
∩![]() ,
,
所以![]() 平面
平面![]() .
.
又![]()
![]() 平面
平面![]() ,所以
,所以![]() .
.
又因為![]() //
//![]() ,所以
,所以![]() .
.
(2)解:連結![]() 、
、![]() ,則
,則![]() .
.

過![]() 作
作![]() 交
交![]() 于
于![]() ,又因為
,又因為![]() 平面
平面![]() ,所以
,所以![]() ,且
,且![]() ∩
∩![]() ,
,
所以![]() 平面
平面![]() ,則
,則![]() 是四棱錐
是四棱錐![]() 的高.
的高.
因為四邊形![]() 是底角為
是底角為![]() 的等腰梯形,
的等腰梯形,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
因為![]() 平面
平面![]() ,
,![]() //
//![]() ,所以
,所以![]() 平面
平面![]() ,則
,則![]() 是三棱錐
是三棱錐![]() 的高.
的高.
所以![]() ,
,
所以![]() .
.
點睛:空間幾何體體積問題的常見類型及解題策略
(1)若所給定的幾何體是可直接用公式求解的柱體、錐體或臺體,則可直接利用公式進行求解.
(2)若所給定的幾何體的體積不能直接利用公式得出,則常用轉換法、分割法、補形法等方法進行求解.
(3)若以三視圖的形式給出幾何體,則應先根據三視圖得到幾何體的直觀圖,然后根據條件求解.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:高中數學 來源: 題型:
【題目】下列“若p,則q”形式的命題中,哪些命題中的q是p的必要條件?
(1)若四邊形為平行四邊形,則這個四邊形的兩組對角分別相等;
(2)若兩個三角形相似,則這兩個三角形的三邊成比例;
(3)若四邊形的對角線互相垂直,則這個四邊形是菱形;
(4)若![]() ,則
,則![]() ;
;
(5)若![]() ,則
,則![]() ;
;
(6)若![]() 為無理數,則x,y為無理數.
為無理數,則x,y為無理數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三角形的三個頂點的坐標分別為![]() ,
,![]() ,
,![]() ,則該三角形的重心(三邊中線交點)的坐標為
,則該三角形的重心(三邊中線交點)的坐標為![]() .類比這個結論,連接四面體的一個頂點及其對面三角形重心的線段稱為四面體的中線,四面體的四條中線交于一點,該點稱為四面體的重心.若四面體的四個頂點的空間坐標分別為
.類比這個結論,連接四面體的一個頂點及其對面三角形重心的線段稱為四面體的中線,四面體的四條中線交于一點,該點稱為四面體的重心.若四面體的四個頂點的空間坐標分別為![]() ,
,![]() ,
,![]() ,
,![]() ,則該四面體的重心的坐標為( )
,則該四面體的重心的坐標為( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高一學年結束后,要對某班的50名學生進行文理分班,為了解數學對學生選擇文理科是否有影響,有人對該班的分科情況做了如下的數據統計:
理科人數 | 文科人數 | 總計 | |
數學成績好的人數 | 25 | 30 | |
數學成績差的人數 | 10 | ||
合計 | 15 |
(Ⅰ)根據數據關系,完成![]() 列聯表;
列聯表;
(Ⅱ)通過計算判斷能否在犯錯誤的概率不超過![]() 的前提下認為數學對學生選擇文理科有影響.
的前提下認為數學對學生選擇文理科有影響.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出n的值為( )(參考數據:sin15°=0.2588,sin7.5°=0.1305)

A. 12B. 24C. 48D. 96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為4,動點E,F在棱
的棱長為4,動點E,F在棱![]() 上,動點P,Q分別在棱AD,CD上。若
上,動點P,Q分別在棱AD,CD上。若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 大于零),則四面體PEFQ的體積
大于零),則四面體PEFQ的體積
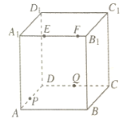
A.與![]() 都有關B.與m有關,與
都有關B.與m有關,與![]() 無關
無關
C.與p有關,與![]() 無關D.與π有關,與
無關D.與π有關,與![]() 無關
無關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出n的值為( )(參考數據:sin15°=0.2588,sin7.5°=0.1305)

A. 12B. 24C. 48D. 96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保護一件珍貴文物,博物館需要在一種無色玻璃的密封保護罩內充入保護氣體.假設博物館需要支付的總費用由兩部分組成:①罩內該種氣體的體積比保護罩的容積少0.5立方米,且每立方米氣體費用1千元;②需支付一定的保險費用,且支付的保險費用與保護罩容積成反比,當容積為2立方米時,支付的保險費用為8千元.
(1)求博物館支付總費用y與保護罩容積V之間的函數關系式;
(2)求博物館支付總費用的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com