【題目】已知三棱錐
的四個頂點在球
的球面上，
，
是邊長為
正三角形，
分別是
的中點，
，則球的體積為_________________。
【答案】
【解析】
由已知設出
，
，
，分別在
中和在
中運用余弦定理表示
，得到關于x與y的關系式，再在
中運用勾股定理得到關于x與y的又一關系式，聯(lián)立可解得x，y，從而分析出正三棱錐是
，
，
兩兩垂直的正三棱錐，所以三棱錐
的外接球就是以為棱的正方體的外接球，再通過正方體的外接球的直徑等于正方體的體對角線的長求出球的半徑，再求出球的體積.
在中，設，，，
,
，
因為點
，點
分別是，
的中點，所以
，
，
在中，
，在中，
，
整理得
，
因為
是邊長為
的正三角形，所以
，
又因為
，所以
，由
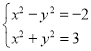，解得
，
所以
。
又因為是邊長為的正三角形，所以
，所以
，
所以，，兩兩垂直，
則球
為以為棱的正方體的外接球，
則外接球直徑為
，
所以球的體積為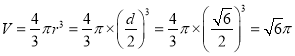
,
故答案為：.
科目：高中數(shù)學 來源： 題型：
【題目】設
且
，則“函數(shù)
在
上是減函數(shù)”是“函數(shù)
在上是增函數(shù)”的（ ）條件．
A. 充分不必要 B. 必要不充分 C. 充要 D. 既不充分也不必要
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在
九章算術
中，將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬
如圖，已知四棱錐
為陽馬，且
，
底面
若E是線段AB上的點
含端點
，設SE與AD所成的角為
，SE與底面ABCD所成的角為
，二面角
的平面角為
，則
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線C：
的焦點為F，M是拋物線C上位于第一象限內的任意一點，O為坐標原點，記經過M，F，O三點的圓的圓心為Q，且點Q到拋物線C的準線的距離為
．
Ⅰ
求點Q的縱坐標；可用p表示
Ⅱ求拋物線C的方程；
Ⅲ設直線l：
與拋物線C有兩個不同的交點A，
若點M的橫坐標為2，且
的面積為
，求直線l的方程．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知
，設
：實數(shù)
滿足
，
：實數(shù)滿足
．
（1）若
，且
為真，求實數(shù)的取值范圍；
（2）若是的必要不充分條件，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】關于函數(shù)
，有下列命題：①當
時，
是增函數(shù)；當
時，是減函數(shù)；②其圖象關于
軸對稱；③無最大值，也無最小值；④在區(qū)間
上是增函數(shù)；⑤的最小值是
。其中所有不正確命題的序號是________
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某地區(qū)經過一年的新農村建設，農村的經濟收入增加了一倍．實現(xiàn)翻番．為更好地了解該地區(qū)農村的經濟收入變化情況，統(tǒng)計了該地區(qū)新農村建設前后農村的經濟收入構成比例．得到如下餅圖：
則下面結論中不正確的是
A. 新農村建設后，種植收入減少
B. 新農村建設后，其他收入增加了一倍以上
C. 新農村建設后，養(yǎng)殖收入增加了一倍
D. 新農村建設后，養(yǎng)殖收入與第三產業(yè)收入的總和超過了經濟收入的一半
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在“新零售”模式的背景下，某大型零售公司咪推廣線下分店，計劃在
市的
區(qū)開設分店，為了確定在該區(qū)開設分店的個數(shù)，該公司對該市已開設分店聽其他區(qū)的數(shù)據作了初步處理后得到下列表格．記
表示在各區(qū)開設分店的個數(shù)， 
表示這個
個分店的年收入之和．
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
（1）該公司已經過初步判斷，可用線性回歸模型擬合
與
的關系，求
關于
的線性回歸方程
；
（2）假設該公司在
區(qū)獲得的總年利潤
（單位：百萬元）與
之間的關系為
，請結合（1）中的線性回歸方程，估算該公司應在
區(qū)開設多少個分時，才能使
區(qū)平均每個分店的年利潤最大？
（參考公式： 
，其中
）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】（題文）如圖，在五面體ABCDEF中，四邊形EDCF是正方形，
．
(1)證明：
；
(2)已知四邊形ABCD是等腰梯形，且
，求五面體ABCDEF的體積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
