【題目】已知
，設實數
、
、
、
、
、
滿足
（i）、、
且不全為0；
（ii）、、
；
（iii）若
，則
.
若所有形如
和
的數均不為2014的倍數，則稱集合
為“好集”.求好集所含元素個數的最大值.
【答案】503
【解析】
（1）構造一個503元好集
.
設
.
若
、
、
均不為0，則
.
于是，
為奇數，一定不為2014的倍數.
若、、中有0，不妨設
，則由條件（i）知、中至少有一個不為0.
由條件（iii）知
.
注意到，
.
故
一定不為2014的倍數.
顯然，
為奇數，一定不為2014的倍數.
則為503元好集.
（2）設
為好集.下面證明：
.
設的最小元素為
.則集合中任意兩元素的差不為.否則，設
、
，
，得
為2014的倍數，矛盾.
將
中大于的元素從大到小每
個分為一組，設可分成
組，余下的
個數為
，
，…，
.
顯然，
，組中的每一組至多有個數在集合中.
由好集的定義，知2014、
，且
與
不同在集合中.
不妨設
，否則，只需將集合中大于1007的元素換成.
事實上，若中有某個
，則將其中的
變為
，將
變為
后得到的數與模2014相同.
下面對
分情形討論.
1）若
，則，，…，中至多有
個數屬于集合.
故
.
2）若
，則
.
從而，任意一個好集必滿足.
由（1）、（2），知好集所含元素個數的最大值為503.
科目：高中數學 來源： 題型：
【題目】某食品廠為了檢查一條自動包裝流水線的生產情況，隨即抽取該流水線上
件產品作為樣本算出他們的重量（單位：克）重量的分組區間為
，
，……
，由此得到樣本的頻率分布直方圖，如圖所示．
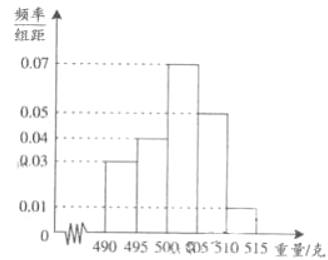
（1）根據頻率分布直方圖，求重量超過
克的產品數量．
（2）在上述抽取的件產品中任取
件，設
為重量超過克的產品數量，求的分布列．
（3）從流水線上任取
件產品，求恰有件產品合格的重量超過克的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ex-x2+a，x∈R，曲線y=f（x）在（0，f（0））處的切線方程為y=bx．
（1）求f（x）的解析式；
（2）當x∈R時，求證：f（x）≥-x2+x；
（3）若f（x）≥kx對任意的x∈（0，+∞）恒成立，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廠生產的某種零件的尺寸
大致服從正態分布
，且規定尺寸
為次品，其余的為正品．生產線上的打包機自動把每5件零件打包成1箱，然后進入銷售環節，若每銷售一件正品可獲利50元，每銷售一件次品虧損100元．現從生產線生產的零件中抽樣20箱做質量分析，作出的頻率分布直方圖如下：
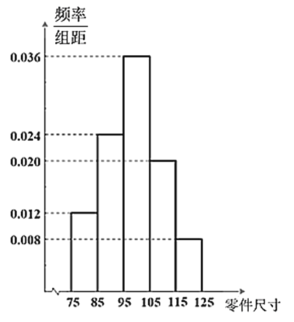
（1）估計生產線生產的零件的次品率及零件的平均尺寸；
（2）從生產線上隨機取一箱零件，求這箱零件銷售后的期望利潤及不虧損的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
個人排成一排，在下列情況下，各有多少種不同排法？
（1）甲不在兩端；
（2）甲、乙、丙三個必須在一起；
（3）甲、乙必須在一起，且甲、乙都不能與丙相鄰．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
,不過原點的直線
與橢圓交于A、B兩點.
(1)求
面積的最大值.
(2)是否存在橢圓
,使得對于橢圓的每一條切線與橢圓
均相交,設交于A、B兩點,且
恰取最大值?若存在,求出該橢圓;若不存在,說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學為研究學生的身體素質與課外體育鍛煉時間的關系，對該校200名學生的課外體育鍛煉平均每天運動的時間（單位：分鐘）進行調查，將收集的數據分成
六組，并作出頻率分布直方圖（如圖），將日均課外體育鍛煉時間不低于40分鐘的學生評價為“課外體育達標”.
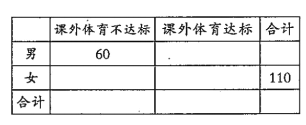
(1)請根據直方圖中的數據填寫下面的
列聯表，并通過計算判斷是否能在犯錯誤的概率不超過0.01的前提下認為“課外體育達標”與性別有關？
（2）現按照“課外體育達標”與“課外體育不達標”進行分層抽樣，抽取8人，再從這8名學生中隨機抽取3人參加體育知識問卷調查，記“課外體育不達標”的人數為
，求
的分布列和數學期望.
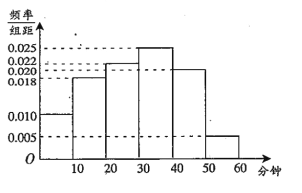
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，直三棱柱ABC-A1B1C1中，D,E分別是AB，BB1的中點.
（Ⅰ）證明： BC1//平面A1CD;
（Ⅱ）設AA1= AC=CB=2，AB=2
，求三棱錐C一A1DE的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
