
【題目】已知函數g(x)=(a+1)x﹣2+1(a>0)的圖象恒過定點A,且點A又在函數 ![]() 的圖象上.
的圖象上.
(1)求實數a的值;
(2)解不等式f(x)< ![]() ;
;
(3)函數h(x)=|g(x+2)﹣2|的圖象與直線y=2b有兩個不同的交點時,求b的取值范圍.
【答案】
(1)解:函數g(x)的圖象恒過定點A,當x﹣2=0時,即x=2,y=2,
∴A點的坐標為(2,2),
又A點在f(x)上,
∴f(2)= ![]() =a,解得a=1
=a,解得a=1
(2)解:)f(x)< ![]() ,
,
∴ ![]() <
< ![]() =0,
=0,
∴0<x+1<1,
∴﹣1<x<0,
∴不等式的解集為(﹣1,0)
(3)解:由(1)知g(x)=g(x)=2x﹣2+1,
∴h(x)=|g(x+2)﹣2|=|2x﹣1|=2b,
分別畫出y=h(x)與y=2b的圖象,如圖所示:
由圖象可知:0<2b<1,故b的取值范圍為 ![]()
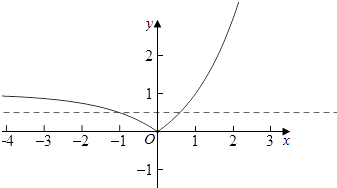
【解析】(1)運用a0=1,令x﹣2=0,則x=2,求得g(2)=2,代入f(x),即可求得a=1;(2)運用對數函數的單調性,當a>1時,f(x)在x>0上遞增,解不等式即可得到;(3)求出h(x),分別畫出y=h(x)與y=2b的圖象,由圖象可知:0<2b<1,即可求出b的范圍.
【考點精析】本題主要考查了指數函數的單調性與特殊點的相關知識點,需要掌握0<a<1時:在定義域上是單調減函數;a>1時:在定義域上是單調增函數才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】如圖,設O是平行四邊形ABCD的兩條對角線AC,BD的交點,下列向量組:
① ![]() 與
與 ![]() ;②
;② ![]() 與
與 ![]() ;
;
③ ![]() 與
與 ![]() ;④
;④ ![]() 與
與 ![]() .
.
其中可作為這個平行四邊形所在平面的一組基底的是( ).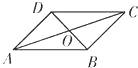
A.①②
B.③④
C.①③
D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為貫徹落實教育部6部門《關于加快發展青少年校園足球的實施意見》,全面提高我市中學生的體質健康水平,培養拼搏意識和團隊精神,普及足球知識和技能,市教體局決定舉行春季校園足球聯賽.為迎接此次聯賽,甲中學選拔了20名學生組成集訓隊,現統計了這20名學生的身高,記錄入如表:(設ξ為隨機變量) 
身高(cm) | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
人數 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
(1)請計算這20名學生的身高的中位數、眾數,并補充完成下面的莖葉圖;
(2)身高為185cm和188cm的四名學生分別記為A,B,C,D,現從這四名學生選2名擔任正副門將,請利用列舉法列出所有可能情況,并求學生A入選門將的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)如圖所示,一根水平放置的長方體枕木的安全負荷與它的厚度d的平方和寬度a的乘積成正比,同時與它的長度![]() 的平方成反比.
的平方成反比.
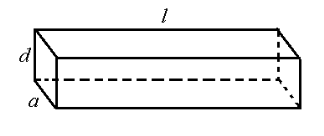
(1)在a>d>0的條件下,將此枕木翻轉90°(即寬度變為了厚度),枕木的安全負荷會發生變化嗎?變大還是變小?
(2)現有一根橫截面為半圓(半圓的半徑為R=![]() )的柱形木材,用它截取成橫截面為長方形的枕木,其長度即為枕木規定的長度l,問橫截面如何截取,可使安全負荷最大?
)的柱形木材,用它截取成橫截面為長方形的枕木,其長度即為枕木規定的長度l,問橫截面如何截取,可使安全負荷最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過直線x=﹣2上的動點P作拋物線y2=4x的兩條切線PA,PB,其中A,B為切點.
(1)若切線PA,PB的斜率分別為k1 , k2 , 求證:k1k2為定值;
(2)求證:直線AB恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若不等式(m﹣1)x2+(m﹣1)x+2>0的解集是R,則m的范圍是( )
A.(1,9)
B.(﹣∞,1]∪(9,+∞)
C.[1,9)
D.(﹣∞,1)∪(9,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產產品x件的總成本c(x)=1200+![]() x3(萬元),已知產品單價P(萬元)與產品件數x滿足:p2=
x3(萬元),已知產品單價P(萬元)與產品件數x滿足:p2=![]() ,生產100件這樣的產品單價為50萬元.
,生產100件這樣的產品單價為50萬元.
(1)設產量為x件時,總利潤為L(x)(萬元),求L(x)的解析式;
(2)產量x定為多少件時總利潤L(x)(萬元)最大?并求最大值(精確到1萬元).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當a=1時,x0∈[1,e]使不等式f(x0)≤m,求實數m的取值范圍;
(2)若在區間(1,+∞)上,函數f(x)的圖象恒在直線y=2ax的下方,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
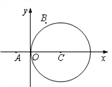
【題目】如圖,在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 及點
及點![]() ,
, ![]() .
.
(1)若直線![]() 平行于
平行于![]() ,與圓
,與圓![]() 相交于
相交于![]() ,
, ![]() 兩點,
兩點, ![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)在圓C上是否存在點P,使得![]() ?若存在,求點P的個數;若不存在,說明理由.
?若存在,求點P的個數;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com