
���}Ŀ����֪�A![]() ���c(di��n)
���c(di��n)![]() ��ֱ��l��
��ֱ��l��![]() �ϵĄ�(d��ng)�c(di��n)�����ڈAC�Ͽ����ڲ�ͬ�ă��c(di��n)A��Bʹ��
�ϵĄ�(d��ng)�c(di��n)�����ڈAC�Ͽ����ڲ�ͬ�ă��c(di��n)A��Bʹ��![]() ���t
���t![]() ��ȡֵ������_____��
��ȡֵ������_____��
���𰸡�![]()
��������
���ڈA![]() �Ͽ����ڲ�ͬ�ă��c(di��n)A��Bʹ��
�Ͽ����ڲ�ͬ�ă��c(di��n)A��Bʹ��![]() ��֪��߅��OAPB�����Σ�����
��֪��߅��OAPB�����Σ�����![]() ��ֱƽ��
��ֱƽ��![]() ��Ȼ����ӑՓ����(d��ng)ֱ��
��Ȼ����ӑՓ����(d��ng)ֱ��![]() ��б�ʞ�0�r(sh��)���˕r(sh��)�ڈA
��б�ʞ�0�r(sh��)���˕r(sh��)�ڈA![]() �ϲ����ڲ�ͬ�ă��c(di��n)
�ϲ����ڲ�ͬ�ă��c(di��n)![]() �M��l������(d��ng)ֱ��
�M��l������(d��ng)ֱ��![]() ��б�ʲ����ڕr(sh��)���ɵ�
��б�ʲ����ڕr(sh��)���ɵ�![]() ���˕r(sh��)ֱ��
���˕r(sh��)ֱ��![]() ���̞��
���̞��![]() ���M��l������(d��ng)ֱ��
���M��l������(d��ng)ֱ��![]() ��б�ʴ����Ҳ���0�r(sh��)������
��б�ʴ����Ҳ���0�r(sh��)������![]() ��
��![]() ���ɵ�ֱ��
���ɵ�ֱ��![]() ���̞�
���̞�![]() ���A�ĵ�ֱ��
���A�ĵ�ֱ��![]() �ľ��x
�ľ��x![]() ����
����![]() ��������
��������![]() �����ɽ��������
�����ɽ��������
���ڈA![]() �Ͽ����ڲ�ͬ�ă��c(di��n)
�Ͽ����ڲ�ͬ�ă��c(di��n)![]() ʹ��
ʹ��![]() ��
��
����߅��OAPB�����Σ�
��ֱ��![]() ��ֱƽ��OP��
��ֱƽ��OP��
�ٮ�(d��ng)ֱ��![]() ��б�ʞ�0�r(sh��)����ֱ��
��б�ʞ�0�r(sh��)����ֱ��![]() ��
��![]() ���˕r(sh��)�ڈA
���˕r(sh��)�ڈA![]() �ϲ����ڲ�ͬ�ă��c(di��n)
�ϲ����ڲ�ͬ�ă��c(di��n)![]() �M��l����
�M��l����
�ڮ�(d��ng)ֱ��![]() ��б�ʲ����ڕr(sh��)����ֱ��
��б�ʲ����ڕr(sh��)����ֱ��![]() �ɵ�
�ɵ�![]() ���˕r(sh��)ֱ��
���˕r(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ���M��l����
���M��l����
�ۮ�(d��ng)ֱ��![]() ��б�ʴ����Ҳ���0�r(sh��)��
��б�ʴ����Ҳ���0�r(sh��)��
��![]() ��
��![]() ��
��
��![]() ��
��
��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ��
��
���}��ÈA�ĵ�ֱ��![]() �ľ��x
�ľ��x![]() ����
����![]() ��
��
��![]() ��
��
��![]() �����
�����![]() ��
��
��![]() ��ȡֵ������
��ȡֵ������![]() ��
��
�ʴ𰸞飺![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���Ї�(gu��)���y(t��ng)�Ļ��кܶ���(n��i)���w�F(xi��n)�˔�(sh��)�W(xu��)�Č�(du��)�Q������D��ʾ��̫�O�D���ɺڰ׃ɂ�(g��)�~�μy�M�ɵĈA�ΈD�������չ�F(xi��n)����D(zhu��n)������(du��)�Q�y(t��ng)һ����ʽ�������C�����o�����x���܉�?q��)��AO�����L(zh��ng)����eͬ�r(sh��)ƽ�ֵĺ���(sh��)�Q���@��(g��)�A�ġ���(y��u)������(sh��)�����o���������}��
����(du��)������һ��(g��)�AO���䡰��(y��u)������(sh��)���Пo(w��)��(sh��)��(g��)��
������(sh��)f��x����ln��![]() ��������ij��(g��)�A�ġ���(y��u)������(sh��)����
��������ij��(g��)�A�ġ���(y��u)������(sh��)����
������(sh��)y��1+sinx����ͬ�r(sh��)�ǟo(w��)��(sh��)��(g��)�A�ġ���(y��u)������(sh��)����
������(sh��)y��2x+1����ͬ�r(sh��)�ǟo(w��)��(sh��)��(g��)�A�ġ���(y��u)������(sh��)����
������(sh��)y��f��x���ǡ���(y��u)������(sh��)���ij�Ҫ�l���麯��(sh��)y��f��x���ĈD�������Č�(du��)�Q�D��.
�������_�����}��_____.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)�E�A![]() ������c(di��n)��
������c(di��n)��![]() ������c(di��n)��
������c(di��n)��![]() .��֪�E�A�Ľ�����
.��֪�E�A�Ľ�����![]() ��ֱ��
��ֱ��![]() ��б�ʞ�
��б�ʞ�![]() .
.
��1����E�A�Ę�(bi��o)��(zh��n)���̣�
��2���O(sh��)ֱ��![]() ��
��![]() ���c�E�A����
���c�E�A����![]() ��
��![]() ���c(di��n)�����c(di��n)
���c(di��n)�����c(di��n)![]() �ڵڶ�����.
�ڵڶ�����.![]() �c
�c![]() ���L(zh��ng)�������c(di��n)
���L(zh��ng)�������c(di��n)![]() ����
����![]() ����e��
����e��![]() ��e��
��e��![]() ������
������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���ڈA�ĽǞ�ֱ�ǵ�����OAB�^(q��)���У�M��N�քe��OA��OB�����c(di��n)����M��N���c(di��n)̎����һ��(g��)ͨ�Ż�վ������̖(h��o)�ĸ��w�����քe����OA��OB��ֱ���ĈA��������OAB��(n��i)�S�C(j��)ȡһ�c(di��n)���t���c(di��n)�o(w��)��̖(h��o)�ĸ�����![]() ��
��![]()
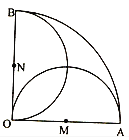
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����������![]() �У�
�У�![]() ߅�L(zh��ng)��
߅�L(zh��ng)��![]() �������Σ�
��������![]() ��
��![]()

��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ��
������ֵ��
��3���C�����ھ���![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ��ʹ��
��ʹ��![]() ������
������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�p����![]() ��һ��(g��)���c(di��n)��
��һ��(g��)���c(di��n)��![]() ����
����![]()
��1�����p����![]() �ķ���
�ķ���
��2���O(sh��)��(j��ng)�^(gu��)���c(di��n)![]() ��ֱ��
��ֱ��![]() ��һ��(g��)��������
��һ��(g��)��������![]() ����(d��ng)ֱ��
����(d��ng)ֱ��![]() �c�p����
�c�p����![]() ����֧�ཻ�ڲ�ͬ�ă��c(di��n)
����֧�ཻ�ڲ�ͬ�ă��c(di��n)![]() �r(sh��)����(sh��)��(sh��)
�r(sh��)����(sh��)��(sh��)![]() ��ȡֵ����
��ȡֵ����
��3���O(sh��)��2����ֱ��![]() �c�p����
�c�p����![]() ����֧�ཻ��
����֧�ཻ��![]() ���c(di��n)����(w��n)�Ƿ���ڌ�(sh��)��(sh��)
���c(di��n)����(w��n)�Ƿ���ڌ�(sh��)��(sh��)![]() ��ʹ��
��ʹ��![]() ���J�ǣ������ڣ�Ո(q��ng)���
���J�ǣ������ڣ�Ո(q��ng)���![]() �ķ������������ڣ�Ո(q��ng)�f(shu��)������
�ķ������������ڣ�Ո(q��ng)�f(shu��)������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��AD�cBC�������wABCD�л��ഹֱ���⣬BC=2. ��AD=2c����AB+BD=AC+CD=2a������a��c�鳣��(sh��)���t�����wABCD���w�e�����ֵ�� .
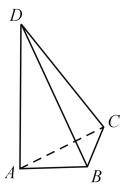
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������f(shu��)�������_�Ă�(g��)��(sh��)�ǣ� ��
�����P(gu��n)ϵ��(sh��)![]() �Á�(l��i)����?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)����
�Á�(l��i)����?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)����![]() Խ�ӽ���1�����P(gu��n)��Խ����
Խ�ӽ���1�����P(gu��n)��Խ����
�ڻؚwֱ��![]() �^(gu��)�ӱ��c(di��n)����
�^(gu��)�ӱ��c(di��n)����![]() ��
��
�����P(gu��n)ָ��(sh��)![]() �Á�(l��i)�̮��ؚw��Ч����
�Á�(l��i)�̮��ؚw��Ч����![]() ԽС���f(shu��)��ģ�͵ĔM��Ч��Խ����.
ԽС���f(shu��)��ģ�͵ĔM��Ч��Խ����.
A. 0B. 1C. 2D. 3
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����D���������w![]() �У��c(di��n)
�У��c(di��n)![]() �քe����
�քe����![]() ��
��![]() �����c(di��n)���c(di��n)
�����c(di��n)���c(di��n)![]() ���ϵ�������ģ��^(gu��)
���ϵ�������ģ��^(gu��)![]() ���c(di��n)��ƽ��������w�֞�ɲ��֣����к�
���c(di��n)��ƽ��������w�֞�ɲ��֣����к�![]() �IJ��֞�
�IJ��֞�![]() ������
������![]() �IJ��֞�
�IJ��֞�![]() ���B��
���B��![]() ��
��![]() ����һ�c(di��n)
����һ�c(di��n)![]() ���O(sh��)
���O(sh��)![]() �cƽ��
�cƽ��![]() ���ɽǞ�
���ɽǞ�![]() ���t
���t![]() �����ֵ�飨 ��
�����ֵ�飨 ��
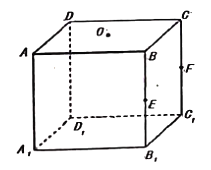
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com