【題目】(本題滿分12分)
已知橢圓
的中心在原點，焦點在
軸上，橢圓上的點到焦點的距離的最
小值為
，離心率為
。
（I）求橢圓
的方程；
（Ⅱ）過點（1，0）作直線
交
于
、
兩點，試問：在
軸上是否存在一個定點
，使
為定值？若存在，求出這個定點
的坐標；若不存在，請說明理由。
【答案】
解：（I）設橢圓E的方程為
由已知得：
2分
橢圓E的方程為
················································3分
（Ⅱ）解：假設存在符合條件的點
，又設
，則：
···················································5分
①當直線
的斜率存在時，設直線
的方程為：
，則
由
得
7分
所以
·················································9分
對于任意的
值，
為定值，
所以
，得
，
所以
；······················································11分
②當直線
的斜率不存在時，直線
由
得
綜上述①②知，符合條件的點
存在，起坐標為
。························12分
【解析】略
科目：高中數學 來源： 題型：
【題目】在某服裝商場，當某一季節即將來臨時，季節性服裝的價格呈現上升趨勢．設一種服裝原定價為每件70元，并且每周(7天)每件漲價6元，5周后開始保持每件100元的價格平穩銷售；10周后，當季節即將過去時，平均每周每件降價6元，直到16周末，該服裝不再銷售．
(1)試建立每件的銷售價格
(單位：元)與周次
之間的函數解析式；
(2)若此服裝每件每周進價
(單位：元)與周次之間的關系為
，
，試問該服裝第幾周的每件銷售利潤最大？(每件銷售利潤＝每件銷售價格－每件進價)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數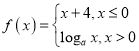
且點
在函數
的圖象上．
（1）求函數的解析式，并在圖中的直角坐標系中畫出函數的圖象；
（2）求不等式
的解集；
（3）若方程
有兩個不相等的實數根，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線x2－
＝1.
(1)若一橢圓與該雙曲線共焦點，且有一交點P(2,3)，求橢圓方程．
(2)設(1)中橢圓的左、右頂點分別為A、B，右焦點為F，直線l為橢圓的右準線，N為l上的一動點，且在x軸上方，直線AN與橢圓交于點M.若AM＝MN，求∠AMB的余弦值；
(3)設過A、F、N三點的圓與y軸交于P、Q兩點，當線段PQ的中點為(0,9)時，求這個圓的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在創建“全國文明衛生城”過程中，某市“創城辦”為了調查市民對創城工作的了解情況，進行了一次創城知識問卷調查(一位市民只能參加一次).通過隨機抽樣，得到參加問卷調查的1000人的得分(滿分100分)統計結果如下表所示.
組別 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
（1）由頻數分布表可以大致認為，此次問卷調查的得分
服從正態分布
， 
近似為這1000人得分的平均值值(同一組數據用該組數據區間的中點值表示)，請用正態分布的知識求
；
（2）在（1）的條件下,“創城辦”為此次參加問卷調查的市民制定如下獎勵方案：:
（ⅰ）得分不低于
的可以獲贈2次隨機話費，得分低于
的可以獲贈1次隨機話費；
（ⅱ）每次獲贈送的隨機話費和對應的概率為：
贈送的隨機話費（單元：元） | 20 | 40 |
概率 | 0.75 | 0.25 |
現有市民甲要參加此次問卷調查，記
(單位：元)為該市民參加問卷調查獲贈的話費,求
的分布列與數學期望.
附：參考數據與公式
，若
，則
①
；
②
；
③
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，
分別是雙曲線
的左頂點、右焦點，過的直線
與
的一條漸近線垂直且與另一條漸近線和
軸分別交于
，
兩點.若
，則的離心率是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標平面中， 
的兩個頂點為
，平面內兩點
、
同時滿足：①
；②
；③
．
（1）求頂點
的軌跡
的方程；
（2）過點
作兩條互相垂直的直線
，直線
與點
的軌跡
相交弦分別為
，設弦
的中點分別為
．
①求四邊形
的面積
的最小值；
②試問：直線
是否恒過一個定點？若過定點，請求出該定點，若不過定點，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝
lnx－x＋
，其中a>0.
(1)若f(x)在(0，＋∞)上存在極值點，求a的取值范圍；
(2)設a∈(1，e]，當x1∈(0,1)，x2∈(1，＋∞)時，記f(x2)－f(x1)的最大值為M(a)．那么M(a)是否存在最大值？若存在，求出其最大值；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
