日韩一区和二区,亚洲激情图片小说视频,国产精品理论在线观看

【題目】在Rt△ABC中，CA=CB=2，M，N是斜邊AB上的兩個動點，且MN= ，則的取值范圍為．

【答案】[ ，2]
【解析】解：以C為坐標原點，CA為x軸建立平面坐標系，
則A（2，0），B（0，2），
∴AB所在直線的方程為：，則y=2﹣x，
設M（a，2﹣a），N（b，2﹣b），且0≤a≤2，0≤b≤2不妨設a＞b，
∵MN= ，
∴（a﹣b）2+（b﹣a）2=2，
∴a﹣b=1，
∴a=b+1，
∴0≤b≤1
∴ =（a，2﹣a）（b，2﹣b）
=2ab﹣2（a+b）+4
=2（b2﹣b+1），0≤b≤1
∴當b=0或b=1時有最大值2；
當b= 時有最小值
∴ 的取值范圍為[ ，2]
所以答案是[ ，2]

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】為建立健全國家學生體質健康監測評價機制，激勵學生積極參加身體鍛煉，教育部印發《國家學生體質健康標準（2014年修訂）》，要求各學校每學期開展覆蓋本校各年級學生的《標準》測試工作，并根據學生每個學期總分評定等級.某校決定針對高中學生，每學期進行一次體質健康測試，以下是小明同學六個學期體質健康測試的總分情況.

學期	1	2	3	4	5	6
總分（分）	512	518	523	528	534	535

（1）請根據上表提供的數據，用相關系數說明與的線性相關程度，并用最小二乘法求出關于的線性回歸方程（線性相關系數保留兩位小數）；

（2）在第六個學期測試中學校根據《標準》，劃定540分以上為優秀等級，已知小明所在的學習小組10個同學有6個被評定為優秀，測試后同學們都知道了自己的總分但不知道別人的總分，小明隨機的給小組內4個同學打電話詢問對方成績，優秀的同學有人，求的分布列和期望.

參考公式：，；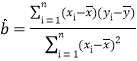

相關系數；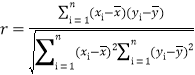

參考數據：，.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】下列命題中正確的命題是（）

A.若存在，當時，有，則說函數在區間上是增函數：

B.若存在（，，、），當時，有，則說函數在區間上是增函數；

C.函數的定義域為，若對任意的，都有，則函數在上一定是減函數：

D.若對任意，當時，有，則說函數在區間上是增函數.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖所示，在四棱錐P﹣ABCD中，AB∥CD，AB⊥AD，AB=AD=AP=2CD=2，M是棱PB上一點．
（Ⅰ）若BM=2MP，求證：PD∥平面MAC；
（Ⅱ）若平面PAB⊥平面ABCD，平面PAD⊥平面ABCD，求證：PA⊥平面ABCD；
（Ⅲ）在（Ⅱ）的條件下，若二面角B﹣AC﹣M的余弦值為，求的值．