
【題目】已知函數(shù)f(x)=2sinωxcosωx+2 ![]() sin2ωx﹣
sin2ωx﹣ ![]() (ω>0)的最小正周期為π. (Ⅰ)求函數(shù)f(x)的單調(diào)增區(qū)間;
(ω>0)的最小正周期為π. (Ⅰ)求函數(shù)f(x)的單調(diào)增區(qū)間;
(Ⅱ)將函數(shù)f(x)的圖象向左平移 ![]() 個單位,再向上平移1個單位,得到函數(shù)y=g(x)的圖象.若y=g(x)在[0,b](b>0)上至少含有10個零點(diǎn),求b的最小值.
個單位,再向上平移1個單位,得到函數(shù)y=g(x)的圖象.若y=g(x)在[0,b](b>0)上至少含有10個零點(diǎn),求b的最小值.
【答案】解:(Ⅰ)由題意,可得
f(x)= ![]() =
= ![]() .
.
∵函數(shù)的最小正周期為π,∴ ![]() =π,解之得ω=1.
=π,解之得ω=1.
由此可得函數(shù)的解析式為 ![]() .
.
令 ![]() ,解之得
,解之得 ![]()
∴函數(shù)f(x)的單調(diào)增區(qū)間是 ![]() .
.
(Ⅱ)將函數(shù)f(x)的圖象向左平移 ![]() 個單位,再向上平移1個單位,可得函數(shù)y=f(x+
個單位,再向上平移1個單位,可得函數(shù)y=f(x+ ![]() )+1的圖象,
)+1的圖象,
∵ ![]()
∴g(x)= ![]() +1=2sin2x+1,可得y=g(x)的解析式為g(x)=2sin2x+1.
+1=2sin2x+1,可得y=g(x)的解析式為g(x)=2sin2x+1.
令g(x)=0,得sin2x=﹣ ![]() ,可得2x=
,可得2x= ![]() 或2x=
或2x= ![]()
解之得 ![]() 或
或 ![]() .
.
∴函數(shù)g(x)在每個周期上恰有兩個零點(diǎn),
若y=g(x)在[0,b]上至少含有10個零點(diǎn),則b不小于第10個零點(diǎn)的橫坐標(biāo)即可,
即b的最小值為 ![]() .
.
【解析】(I)根據(jù)二倍角的三角函數(shù)公式與輔助角公式化簡得 ![]() ,利用周期公式算出ω=1,得函數(shù)解析式為
,利用周期公式算出ω=1,得函數(shù)解析式為 ![]() .再由正弦函數(shù)單調(diào)區(qū)間的公式,解關(guān)于x的不等式即可得到函數(shù)f(x)的單調(diào)增區(qū)間;(II)根據(jù)函數(shù)圖象平移的公式,得出函數(shù)g(x)的解析式為g(x)=2sin2x+1.由此解g(x)=0得sin2x=﹣
.再由正弦函數(shù)單調(diào)區(qū)間的公式,解關(guān)于x的不等式即可得到函數(shù)f(x)的單調(diào)增區(qū)間;(II)根據(jù)函數(shù)圖象平移的公式,得出函數(shù)g(x)的解析式為g(x)=2sin2x+1.由此解g(x)=0得sin2x=﹣ ![]() ,利用正弦函數(shù)的圖象解出
,利用正弦函數(shù)的圖象解出 ![]() 或
或 ![]() ,可見g(x)在每個周期上恰有兩個零點(diǎn),若g(x)在[0,b]上至少含有10個零點(diǎn),則b大于或等于g(x)在原點(diǎn)右側(cè)的第10個零點(diǎn),由此即可算出b的最小值.
,可見g(x)在每個周期上恰有兩個零點(diǎn),若g(x)在[0,b]上至少含有10個零點(diǎn),則b大于或等于g(x)在原點(diǎn)右側(cè)的第10個零點(diǎn),由此即可算出b的最小值.
【考點(diǎn)精析】通過靈活運(yùn)用兩角和與差的正弦公式和正弦函數(shù)的單調(diào)性,掌握兩角和與差的正弦公式:![]() ;正弦函數(shù)的單調(diào)性:在
;正弦函數(shù)的單調(diào)性:在![]()
![]() 上是增函數(shù);在
上是增函數(shù);在![]()
![]() 上是減函數(shù)即可以解答此題.
上是減函數(shù)即可以解答此題.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業(yè)本系列答案
黃岡課堂作業(yè)本系列答案 單元加期末復(fù)習(xí)先鋒大考卷系列答案
單元加期末復(fù)習(xí)先鋒大考卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列函數(shù)中,是奇函數(shù)且在(0,+∞)上單調(diào)遞減的是( )
A.y=x﹣1
B.y=( ![]() )x
)x
C.y=x3
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,側(cè)面BB1C1C為菱形,AB⊥B1C. (Ⅰ)證明:AC=AB1;
(Ⅱ)若AC⊥AB1 , ∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.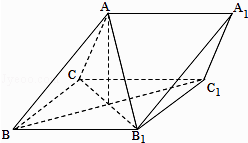
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若偶函數(shù)f(x)在區(qū)間[﹣1,0]上是減函數(shù),α,β是銳角三角形的兩個內(nèi)角,且α≠β,則下列不等式中正確的是( )
A.f(cosα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(cosα)<f(sinβ)
D.f(sinα)>f(sinβ)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=Asin(ωx+φ),(x∈R,A>0,ω>0,|φ|< ![]() )的部分圖象如圖所示:
)的部分圖象如圖所示: 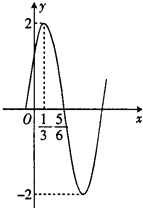
(1)試確定f(x)的解析式;
(2)若f( ![]() )=
)= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù) ![]() 的圖象,經(jīng)過下列哪個平移變換,可以得到函數(shù)y=5sin2x的圖象?( )
的圖象,經(jīng)過下列哪個平移變換,可以得到函數(shù)y=5sin2x的圖象?( )
A.向右平移 ![]()
B.向左平移 ![]()
C.向右平移 ![]()
D.向左平移 ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=x2﹣2x,g(x)=ax+2(a>0),對x1∈[﹣1,2],x0∈[﹣1,2],使g(x1)=f(x0),則a的取值范圍是( )
A.![]()
B.![]()
C.[3,+∞)
D.(0,3]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知冪函數(shù)f(x)=(﹣2m2+m+2)xm+1為偶函數(shù).
(1)求f(x)的解析式;
(2)若函數(shù)y=f(x)﹣2(a﹣1)x+1在區(qū)間(2,3)上為單調(diào)函數(shù),求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商人如果將進(jìn)貨單價(jià)為 ![]() 元的商品按每件
元的商品按每件 ![]() 元出售,則每天可銷售
元出售,則每天可銷售 ![]() 件,現(xiàn)在他采用提高售價(jià),減少進(jìn)貨量的辦法增加利潤.已知這種商品每件銷售價(jià)提高
件,現(xiàn)在他采用提高售價(jià),減少進(jìn)貨量的辦法增加利潤.已知這種商品每件銷售價(jià)提高 ![]() 元,銷售量就要減少
元,銷售量就要減少 ![]() 件,如果使得每天所賺的利潤最大,那么他應(yīng)將每件的銷售價(jià)定為( )
件,如果使得每天所賺的利潤最大,那么他應(yīng)將每件的銷售價(jià)定為( )
A.![]() 元
元
B.![]() 元
元
C.![]() 元
元
D.![]() 元
元
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com