(本小題滿分12分)設(shè)等比數(shù)列

的公比為

,前n項和
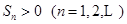
。
(Ⅰ)求

的取值范圍;
(Ⅱ)設(shè)
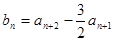
,記
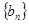
的前n項和為

,試比較

與

的大小。
(Ⅰ)
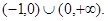
(Ⅱ)當(dāng)
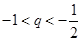
或
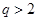
時,
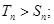
當(dāng)
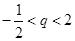
,
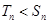
;當(dāng)
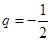
或

=2時,
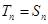
試題分析:(Ⅰ)因為
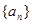
是等比數(shù)列,
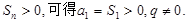
當(dāng)

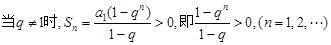
上式等價于不等式組:
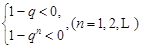
① 或
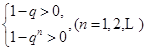
②
解①式得q>1;解②,由于n可為奇數(shù)、可為偶數(shù),得-1<q<1.
綜上,q的取值范圍是
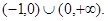
……6分
(Ⅱ)由
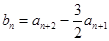
得
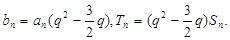
于是
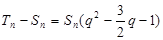
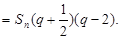
又∵
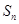
>0且-1<

<0或

>0
當(dāng)
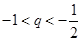
或
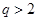
時,
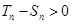
即
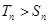
當(dāng)
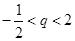
且

≠0時,
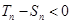
即
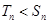
當(dāng)
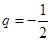
或

=2時,
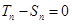
即
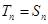
. ……12分
點評:應(yīng)用等比數(shù)列的前n項和公式時,要注意公比是否為1,必要時要分情況討論;比較兩個數(shù)或兩個式子的大小時,常用的方法是作差法或作商法.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
各項均為正數(shù)的等比數(shù)列

,

,

,單調(diào)增數(shù)列

的前

項和為

,

,且

(

).
(Ⅰ)求數(shù)列

、

的通項公式;
(Ⅱ)令

(

),求使得

的所有

的值,并說明理由.
(Ⅲ) 證明

中任意三項不可能構(gòu)成等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
等比數(shù)列{a
n}中,a
7=10,q=-2,則a
10 =( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本題滿分12分)設(shè)數(shù)列
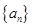
的前
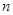
項和為
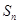
,滿足
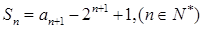
,且
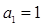
。
(Ⅰ)求
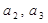
的值;
(Ⅱ)求數(shù)列
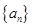
的通項公式;
(Ⅲ)設(shè)數(shù)列
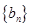
的前
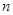
項和為
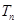
,且
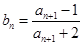
,證明:對一切正整數(shù)
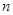
, 都有:
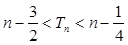
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
已知數(shù)列{a
n}的前n項和為S
n,點
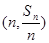
在直線
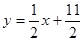
上.數(shù)列{b
n}滿足
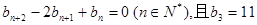
,前9項和為153.
(Ⅰ)求數(shù)列{a
n}、{b
n}的通項公式;
(Ⅱ)設(shè)
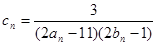
,數(shù)列{c
n}的前n和為T
n,求使不等式
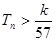
對一切
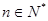
都成立的最大正整數(shù)k的值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知等比數(shù)列
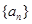
的公比為正數(shù),且
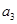
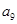
=2
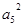
,
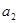
=1,則
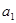
=( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
若等比數(shù)列
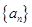
的前
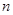
項和為
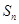
,
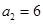
,
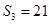
,求數(shù)列
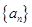
的通項公式。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分16分)數(shù)列{an}的前n項和為Sn(n∈N*),點(an,Sn)在直線y=2x-3n上.
(1)若數(shù)列{an+c}成等比數(shù)列,求常數(shù)c的值;
(2)求數(shù)列{an}的通項公式;
(3)數(shù)列{an}中是否存在三項,它們可以構(gòu)成等差數(shù)列?若存在,請求出一組適合條件的項;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
記等比數(shù)列
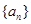
的前
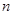
項和為
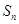
,若
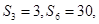
則
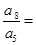
( )
| A. 9 | B.27 | C.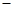 8 8 | D.8 |
查看答案和解析>>

 的公比為
的公比為 ,前n項和
,前n項和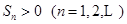 。
。 的取值范圍;
的取值范圍;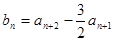 ,記
,記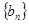 的前n項和為
的前n項和為 ,試比較
,試比較 與
與 的大小。
的大小。 閱讀快車系列答案
閱讀快車系列答案 ,
, ,
, ,單調(diào)增數(shù)列
,單調(diào)增數(shù)列 的前
的前 項和為
項和為 ,
, ,且
,且 (
( ).
). 、
、 的通項公式;
的通項公式; (
( ),求使得
),求使得 的所有
的所有 的值,并說明理由.
的值,并說明理由. 中任意三項不可能構(gòu)成等差數(shù)列.
中任意三項不可能構(gòu)成等差數(shù)列.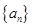 的前
的前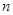 項和為
項和為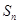 ,滿足
,滿足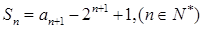 ,且
,且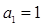 。
。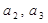 的值;
的值;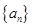 的通項公式;
的通項公式;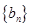 的前
的前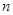 項和為
項和為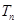 ,且
,且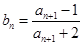 ,證明:對一切正整數(shù)
,證明:對一切正整數(shù)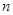 , 都有:
, 都有: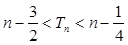
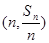 在直線
在直線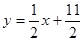 上.數(shù)列{bn}滿足
上.數(shù)列{bn}滿足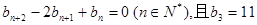 ,前9項和為153.
,前9項和為153.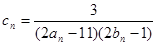 ,數(shù)列{cn}的前n和為Tn,求使不等式
,數(shù)列{cn}的前n和為Tn,求使不等式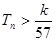 對一切
對一切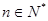 都成立的最大正整數(shù)k的值.
都成立的最大正整數(shù)k的值.