
【題目】已知二次函數![]() 的對稱軸為
的對稱軸為![]() ,
,![]() .
.
(1)求函數![]() 的最小值及取得最小值時
的最小值及取得最小值時![]() 的值;
的值;
(2)試確定![]() 的取值范圍,使
的取值范圍,使![]() 至少有一個實根;
至少有一個實根;
(3)若![]() ,存在實數
,存在實數![]() ,對任意
,對任意![]() ,使
,使![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,此時
,此時![]() ;(2)
;(2)![]() 的取值范圍為
的取值范圍為![]() ;(3)實數
;(3)實數![]() 的取值范圍為
的取值范圍為![]() .
.
【解析】
試題分析:(1)利用基本不等式易得![]() ,此時
,此時![]() .(2)
.(2)![]() 至少有一個實根,即
至少有一個實根,即![]() 與
與![]() 的圖象在
的圖象在![]() 上至少有一個交點,由題意,可得
上至少有一個交點,由題意,可得![]() ,
,![]() ,則需
,則需![]() 即可;(3)由題意,可得
即可;(3)由題意,可得![]() ,則
,則![]() ,
,
由已知存在實數![]() ,對任意
,對任意![]() ,使
,使![]() 恒成立.即
恒成立.即![]() .令
.令![]() ∴
∴![]() ,轉化為存在
,轉化為存在![]() ,使
,使![]() 成立.令
成立.令![]() ,
,![]() 的對稱軸為
的對稱軸為![]() ,分類討論,即可得到實數
,分類討論,即可得到實數![]() 的取值范圍
的取值范圍
試題解析:(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,當且僅當
,當且僅當![]() ,即
,即![]() 時“=”成立,即
時“=”成立,即![]() ,此時
,此時![]() .
.
(2)![]() 的對稱軸為
的對稱軸為![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]() 至少有一個實根,∴
至少有一個實根,∴![]() 至少有一個實根,
至少有一個實根,
即![]() 與
與![]() 的圖象在
的圖象在![]() 上至少有一個交點,
上至少有一個交點,
![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 的取值范圍為
的取值范圍為![]() .
.
(3)![]() ,∴
,∴![]() ,
,
由已知存在實數![]() ,對任意
,對任意![]() ,使
,使![]() 恒成立.
恒成立.
∴![]() .
.
令![]() ,∴
,∴![]() ,即
,即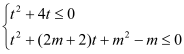 ,
,
轉化為存在![]() ,使
,使![]() 成立.
成立.
令![]() ,∴
,∴![]() 的對稱軸為
的對稱軸為![]() ,
,
∵![]() ,∴
,∴![]() .
.
①當![]() ,即
,即![]() 時,
時,
![]() ,
,
∴![]() ,∴
,∴![]() .
.
②當![]() ,即
,即![]() 時,
時,
![]() ,
,
∴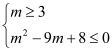 ,∴
,∴![]() ,∴
,∴![]() .
.
綜上,實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,某動物園要建造兩間完全相同的矩形熊貓居室,其總面積為24平方米,設熊貓居室的一面墻![]() 長為
長為![]() 米(2
米(2![]() ).
).
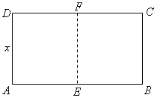
⑴用![]() 表示墻
表示墻![]() 的長;
的長;
⑵假設所建熊貓居室的墻壁造價(在墻壁高度一定的前提下)為每米1000元,請將墻壁的總造價![]() (元)表示為
(元)表示為![]() (米)的函數;
(米)的函數;
⑶當![]() 為何值時,墻壁的總造價最低?
為何值時,墻壁的總造價最低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為方便市民休閑觀光,市政府計劃在半徑為200米,圓心角為![]() 的扇形廣場內(如圖所示),沿
的扇形廣場內(如圖所示),沿![]() 邊界修建觀光道路,其中
邊界修建觀光道路,其中![]() 分別在線段
分別在線段![]() 上,且
上,且![]() 兩點間距離為定長
兩點間距離為定長![]() 米.
米.
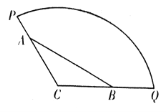
(1)當![]() 時,求觀光道
時,求觀光道![]() 段的長度;
段的長度;
(2)為提高觀光效果,應盡量增加觀光道路總長度,試確定圖中![]() 兩點的位置,使觀光道路總長度達到最長?并求出總長度的最大值.
兩點的位置,使觀光道路總長度達到最長?并求出總長度的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,GH是東西方向的公路北側的邊緣線,某公司準備在GH上的一點B的正北方向的A處建設一倉庫,設![]() ,并在公路北側建造邊長為
,并在公路北側建造邊長為![]() 的正方形無頂中轉站CDEF(其中EF在GH上),現從倉庫A向GH和中轉站分別修兩條道路AB,AC,已知AB=AC+1,且
的正方形無頂中轉站CDEF(其中EF在GH上),現從倉庫A向GH和中轉站分別修兩條道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 關于
關于![]() 的函數解析式,并求出定義域;
的函數解析式,并求出定義域;
(2)如果中轉站四堵圍墻造價為10萬元/km,兩條道路造價為30萬元/km,問:![]() 取何值時,該公司建設中轉站圍墻和兩條道路總造價M最低.
取何值時,該公司建設中轉站圍墻和兩條道路總造價M最低.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(必須列式,不能只寫答案,答案用數字表示)有4個不同的球,四個不同的盒子,把球全部放入盒內.
(1)求共有多少種放法;
(2)求恰有一個盒子不放球,有多少種放法;
(3)求恰有兩個盒內不放球,有多少種放法;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,四邊形ABCD是矩形,側面PAD⊥底面ABCD,若點E,F分別是PC,BD的中點。
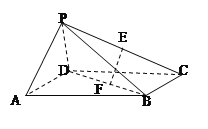
(1)求證:EF∥平面PAD;
(2)求證:平面PAD⊥平面PCD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com