
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的極值;
的極值;
(2)設(shè)![]() ,比較
,比較![]() 與1的大小關(guān)系,并說(shuō)明理由.
與1的大小關(guān)系,并說(shuō)明理由.
【答案】(1)當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 無(wú)極值,當(dāng)
無(wú)極值,當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有極大值
有極大值![]() ,無(wú)極小值;(2)
,無(wú)極小值;(2)![]() ,理由見解析.
,理由見解析.
【解析】
試題分析:(1)依題意![]() ,分子是一個(gè)二次項(xiàng)系數(shù)含有參數(shù)的式子,所以要對(duì)
,分子是一個(gè)二次項(xiàng)系數(shù)含有參數(shù)的式子,所以要對(duì)![]() 進(jìn)行分類討論,根據(jù)開口方向,將
進(jìn)行分類討論,根據(jù)開口方向,將![]() 分成
分成![]() 和
和![]() 兩類來(lái)討論函數(shù)的單調(diào)區(qū)間和極值;(2)
兩類來(lái)討論函數(shù)的單調(diào)區(qū)間和極值;(2)![]() ,即比較
,即比較![]() 與
與![]() 的大小. 令
的大小. 令![]() ,即比較
,即比較![]() 與
與![]() 的大小.構(gòu)造函數(shù)
的大小.構(gòu)造函數(shù)![]() 利用導(dǎo)數(shù)求得其最大值為
利用導(dǎo)數(shù)求得其最大值為![]() ,得證.
,得證.
試題解析:
(1)依題意![]()
①若![]() ,則
,則![]() 在
在![]() 上恒成立,函數(shù)
上恒成立,函數(shù)![]() 無(wú)極值;
無(wú)極值;
②若![]() ,則
,則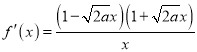 ,此時(shí)
,此時(shí)![]() ,
,
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
故函數(shù)![]() 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為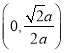 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為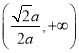 ,
,
故函數(shù)![]() 的極大值為
的極大值為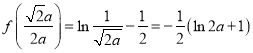 ,無(wú)極小值.
,無(wú)極小值.
綜上所述,當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 無(wú)極值;當(dāng)
無(wú)極值;當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有極大值
有極大值![]() ,無(wú)極小值
,無(wú)極小值
(2)依題意,![]() ,
,
要比較![]() 與1的大小 ,即比較
與1的大小 ,即比較![]() 與
與![]() 的大小.
的大小.
∵![]() ,∴可比較
,∴可比較![]() 與
與![]() 的大小
的大小
令![]() ,即比較
,即比較![]() 與
與![]() 的大小.
的大小.
設(shè)![]() ,
,
則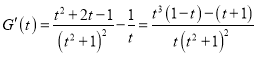 ,
,
因?yàn)?/span>![]() ,所以
,所以![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
故![]() ,所以
,所以![]() 對(duì)任意
對(duì)任意![]() 恒成立,
恒成立,
所以![]() ,
,
所以![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某中學(xué)高三數(shù)學(xué)奧林匹克競(jìng)賽集訓(xùn)隊(duì)的一次數(shù)學(xué)測(cè)試成績(jī)的莖葉圖(圖1)和頻率分布直方圖(圖2)都受到不同程度的破壞,可見部分如圖所示,據(jù)此解答如下問題.
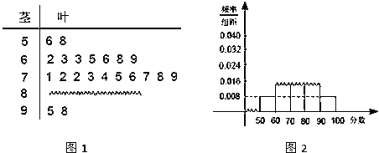
(1)求該集訓(xùn)隊(duì)總人數(shù)及分?jǐn)?shù)在[80,90)之間的頻數(shù);
(2)計(jì)算頻率分布直方圖中[80,90)的矩形的高;
(3)若要從分?jǐn)?shù)在[80,100]之間的試卷中任取兩份分析學(xué)生的答題情況,在抽取的試卷中,求至少有一份分?jǐn)?shù)在[90,100]之間的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() .
.
(1)當(dāng)![]() 時(shí),求曲線
時(shí),求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線的斜率;
處的切線的斜率;
(2)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的單調(diào)區(qū)間與極值.
的單調(diào)區(qū)間與極值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某投資商到一開發(fā)區(qū)投資72萬(wàn)元建起一座蔬菜加工廠,第一年共支出12萬(wàn)元,以后每年支出增加4萬(wàn)元,從第一年起每年的蔬菜銷售收入均為50萬(wàn)元,設(shè)![]() 表示前
表示前![]() 年的純利潤(rùn)總和(
年的純利潤(rùn)總和(![]() =前
=前![]() 年的總收入
年的總收入![]() 前
前![]() 年的總支出
年的總支出![]() 投資額).
投資額).
(1)該廠從第幾年開始盈利?
(2)若干年后,投資商為開發(fā)新項(xiàng)目,對(duì)該廠有兩種處理方案:
① 當(dāng)年平均利潤(rùn)達(dá)到最大時(shí),以48萬(wàn)元出售該廠;
② 當(dāng)純利潤(rùn)總和達(dá)到最大時(shí),以16萬(wàn)元出售該廠,
問哪種方案更合算?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=ax2+bx(a≠0)的導(dǎo)函數(shù)f′(x)=-2x+7,數(shù)列{an}的前n項(xiàng)和為Sn,點(diǎn)Pn(n,Sn)(n∈N*)均在函數(shù)y=f(x)的圖象上,求數(shù)列{an}的通項(xiàng)公式及Sn的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)![]() 的對(duì)稱軸為
的對(duì)稱軸為![]() ,
,![]() .
.
(1)求函數(shù)![]() 的最小值及取得最小值時(shí)
的最小值及取得最小值時(shí)![]() 的值;
的值;
(2)試確定![]() 的取值范圍,使
的取值范圍,使![]() 至少有一個(gè)實(shí)根;
至少有一個(gè)實(shí)根;
(3)若![]() ,存在實(shí)數(shù)
,存在實(shí)數(shù)![]() ,對(duì)任意
,對(duì)任意![]() ,使
,使![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)![]() 的對(duì)稱軸為
的對(duì)稱軸為![]() ,
,![]() .
.
(1)求函數(shù)![]() 的最小值及取得最小值時(shí)
的最小值及取得最小值時(shí)![]() 的值;
的值;
(2)試確定![]() 的取值范圍,使
的取值范圍,使![]() 至少有一個(gè)實(shí)根;
至少有一個(gè)實(shí)根;
(3)當(dāng)![]() 時(shí),
時(shí),![]() ,對(duì)任意
,對(duì)任意![]() 有
有![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,側(cè)面
,側(cè)面![]() 是邊長(zhǎng)為2的等邊三角形,點(diǎn)
是邊長(zhǎng)為2的等邊三角形,點(diǎn)![]() 是
是![]() 的中點(diǎn),且平面
的中點(diǎn),且平面![]() 平面
平面![]() .
.
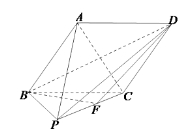
(I)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(II)若點(diǎn)![]() 在線段
在線段![]() 上移動(dòng),是否存在點(diǎn)
上移動(dòng),是否存在點(diǎn)![]() 使平面
使平面![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ?若存在,指出點(diǎn)
?若存在,指出點(diǎn)![]() 的位置,否則說(shuō)明理由.
的位置,否則說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() 實(shí)數(shù)
實(shí)數(shù)![]() 滿足不等式
滿足不等式![]() 函數(shù)
函數(shù)![]() 無(wú)極值點(diǎn).
無(wú)極值點(diǎn).
(1)若“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實(shí)數(shù)
”為真命題,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)已知“![]() ”為真命題,并記為
”為真命題,并記為![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分條件,求正整數(shù)
的必要不充分條件,求正整數(shù)![]() 的值.
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com