【題目】已知函數f（x）
．
（1）畫出函數f（x）的圖象，根據圖象直接寫出f（x）的值域；
（2）根據圖象直接寫出滿足f（x）≥2的所有x的集合；
（3）若f（x）的遞減區間為（﹣∞，a），遞增區間為（b，+∞），直接寫出a的最大值，b的最小值．
【答案】（1）圖見解析，值域為：[0，+∞）；（2）（﹣∞，﹣1]∪[1，+∞）；（3）a的最大值為0，b的最小值為0．
【解析】
（1）根據分段函數解析式，畫出函數圖象，并根據圖象求得函數
的值域.
（2）根據圖象，求得不等式
的解集.
（3）根據圖象，由圖求得函數的單調區間，進而求得
的最大值和
的最小值.
（1）因為函數f（x）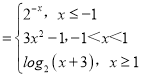
．
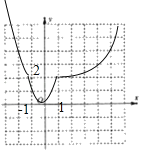
所以：函數f（x）的圖象如圖：；由圖可知其值域為：[0，+∞）；
（2）滿足f（x）≥2的所有x的集合是：（﹣∞，﹣1]∪[1，+∞）；
（3）因為函數的遞減區間為：（﹣∞，0]；遞增區間為：[0，+∞）；
f（x）的遞減區間為（﹣∞，a），遞增區間為（b，+∞）
∴a的最大值為0，b的最小值為0．
科目：高中數學 來源： 題型：
【題目】已知定點
，定直線
： 
，動圓
過點
，且與直線
相切.
（Ⅰ）求動圓
的圓心軌跡
的方程；
（Ⅱ）過點
的直線與曲線
相交于
， 
兩點，分別過點
， 
作曲線
的切線
， 
，兩條切線相交于點
，求
外接圓面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
的參數方程： 
（
為參數)，曲線
的參數方程： 
（
為參數)，且直線交曲線
于
兩點.
(1)將曲線
的參數方程化為普通方程，并求
時， 
的長度；
(2)巳知點
，求當直線傾斜角
變化時， 
的范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在（0，+∞）上的單調函數f（x），x∈（0，+∞），f[f（x）﹣lnx]=1，則方程f（x）﹣f′（x）=1的解所在區間是 （ ）
A. （2，3） B. 
C. 
D. （1，2）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C：x2+y2﹣4y+1＝0，點M（﹣1，﹣1），從圓C外一點P向該圓引一條切線，記切點為T．
（1）若過點M的直線l與圓交于A，B兩點且|AB|＝2
，求直線l的方程；
（2）若滿足|PT|＝|PM|，求使|PT|取得最小值時點P的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人進行象棋比賽，約定先連勝兩局者直接贏得比賽，若賽完5局仍未出現連勝，則判定獲勝局數多者贏得比賽．假設每局甲獲勝的概率為
，乙獲勝的概率為
，各局比賽結果相互獨立．
（1）求甲在4局以內（含4局）贏得比賽的概率；
（2）用X表示比賽決出勝負時的總局數，求隨機變量X的分布列和均值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
