【題目】已知△ABC是銳角三角形，cos22A+sin2A=1.
（Ⅰ）求角A；
（Ⅱ）若BC=1，B=x，求△ABC的周長f（x）的單調區間.
【答案】(Ⅰ)
；(Ⅱ) 單調增區間是（0，
]，單調減區間是[
，
）.
【解析】
試題分析：(Ⅰ)由已知cos22A+sin2A=1，把左邊的一項移到右邊，應用同角關系式化簡，再用二倍角公式變形，可求得A角；(Ⅱ)由正弦定理求出另兩邊長，得周長
，由兩角和的正弦公式化
為一個三角函數形式，再由正弦函數的單調性可得單調區間，求解時要注意函數的定義域.
試題解析：(Ⅰ)∵cos22A+sin2A=1，
∴cos22A=cos2A∴cos2A=±cosA，∴2cos2A﹣1±cosA=0，
∵△ABC是銳角三角形，∴cosA=
，∴A=
.
(Ⅱ)∵BC=1，B=x，
∴AC=
sinx，AB=cosx+
sinx，
∴△ABC的周長f（x）=1+cosx+
sinx=1+2sin（x+
），
∴當﹣
+2kπ≤x+
≤+2kπ，（k∈Z）時，x∈[﹣
+2kπ，
+2kπ]，
∵x∈（0，）∴f（x）的單調增區間是（0，
]，單調減區間是[，）.
教學練新同步練習系列答案
課前課后同步練習系列答案
課堂小作業系列答案
黃岡小狀元口算速算練習冊系列答案
成功訓練計劃系列答案
倍速訓練法直通中考考點系列答案科目：高中數學 來源： 題型：
【題目】某玩具生產公司每天計劃生產衛兵、騎兵、傘兵這三種玩具共100個，生產一個衛兵需5分鐘，生產一個騎兵需7分鐘，生產一個傘兵需4分鐘，已知總生產時間不超過10小時．若生產一個衛兵可獲利潤5元，生產一個騎兵可獲利潤6元，生產一個傘兵可獲利潤3元．
（1）用每天生產的衛兵個數x與騎兵個數y表示每天的利潤W（元）；
（2）怎樣分配生產任務才能使每天的利潤最大，最大利潤是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知在數列{an}中，Sn為其前n項和，若an＞0，且4Sn=an2+2an+1（n∈N*），數列{bn}為等比數列，公比q＞1，b1=a1，且2b2，b4，3b3成等差數列．
（1）求{an}與{bn}的通項公式；
（2）令cn=
，若{cn}的前項和為Tn，求證：Tn＜6．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）記
，求證：函數
在區間
內有且僅有一個零點；
（2）用
表示
中的最小值，設函數
，若關于
的方程
（其中
為常數）在區間有兩個不相等的實根
，記在內的零點為
，試證明：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（Ⅰ）當
時，求函數
的單調區間；
（Ⅱ）若函數
的圖象在點
處的切線的傾斜角為
，且函數
當且僅當在
處取得極值，其中
為
的導函數，求
的取值范圍；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，A,B,C三地有直道相通，AB=5千米，AC=3千米，BC=4千米.現甲、乙兩警員同時從A地出發勻速前往B地，經過t小時，他們之間的距離為
（單位：千米）.甲的路線是AB，速度是5千米/小時，乙的路線是ACB，速度是8千米/小時，乙到達B地后原地等待，設
時，乙到達C地.
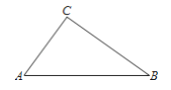
（1）求
與
的值；
（2）已知警員的對講機的有效通話距離是3千米.當
時，求
的表達式，并判斷
在
上的最大值是否超過3？并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知直線
：
（
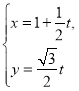為參數），曲線
：
（
為參數）．
（1）設
與
相交于
，
兩點，求
；
（2）若把曲線
上各點的橫坐標壓縮為原來的
倍，縱坐標壓縮為原來的
倍，得到曲線
，設點
是曲線
上的一個動點，求它到直線
距離的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
在
上為增函數,且
,
為常數, 
.
(1)求
的值;(2)若
在上為單調函數,求
的取值范圍;
(3)設
,若在
上至少存在一個
，使得
成立，求的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
