
【題目】設![]() ,
,![]() ,其中實數
,其中實數![]()
(1)若![]() ,求函數
,求函數![]() 的單調區間;
的單調區間;
(2)若函數![]() 與
與![]() 的圖象只有一個公共點,且
的圖象只有一個公共點,且![]() 存在最小值時,記
存在最小值時,記![]() 的最小值為
的最小值為![]() ,求
,求![]() 的值域;
的值域;
(3)若![]() 與
與![]() 均在區間
均在區間![]() 內為增函數,求
內為增函數,求![]() 的取值范圍。
的取值范圍。
【答案】(1)遞減區間為![]() ;遞增區間為
;遞增區間為![]() (2)
(2)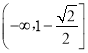 .(3)a≤﹣3或a≥1.
.(3)a≤﹣3或a≥1.
【解析】
(1)由f'(x)=3x2+2ax﹣a2=(3x﹣a)(x+a),a>0,由f′(x)>0,得x![]() .由此能求出f(x)的單調區間.
.由此能求出f(x)的單調區間.
(2)g(x)對稱軸為![]() ,當a>0時,a
,當a>0時,a![]() 且a
且a![]() ;當a<0時,a+2
;當a<0時,a+2![]() 且a+2
且a+2![]() .由此能求出實數a的取值范圍.
.由此能求出實數a的取值范圍.
(3)由已知條件知x3﹣(a2﹣2)x=0只有一個實根,得到a的范圍,再利用二次函數y=g(x)有最小值,由此能求出h(a)的值域.
(1)∵f(x)=x3+ax2﹣a2x+1,
∴f'(x)=3x2+2ax﹣a2=(3x﹣a)(x+a),
∵a>0,∴由f′(x)>0,得x![]() .
.
∴f(x)的遞減區間為![]() ;
;
遞增區間為![]()
(2)由函數y=f(x),y=g(x)關于x方程:x3+ax2﹣a2x+1=ax2﹣2x+1,
即x3﹣(a2﹣2)x=0只有一個實根,x=0滿足題意,
∴x2﹣(a2﹣2)=0在x![]() 時無根,
時無根,
∴a2﹣2≤0,解得![]() .
.
二次函數y=g(x)存在最小值,
∴a>0,∴![]()
∵g(x)=ax2﹣2x+1=a(x![]() )2
)2![]() 1,
1,
∴![]() ,∴h(a)的值域為
,∴h(a)的值域為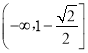 .
.
(3)∵g(x)=ax2﹣2x+1=a(x![]() )2
)2![]() 1,
1,
∴對稱軸為![]() ,
,
當a>0時,由(1)知f(x)的遞增區間為![]() ,
,
∵g(x)在![]() 遞增,
遞增,
依題意![]() ,
,
且(a,a+2)(![]() ),∴a
),∴a![]() 且a
且a![]() ,解得a≥1.
,解得a≥1.
當a<0時,f(x)的遞增區間為![]() ,
,
g(x)在![]() 遞增,
遞增,
依題意![]() 且(a,a+2)(﹣∞,
且(a,a+2)(﹣∞,![]() ),
),
∴a+2![]() 且a+2
且a+2![]() ,解得a≤﹣3.
,解得a≤﹣3.
∴實數a的取值范圍為a≤﹣3或a≥1.


 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源: 題型:
【題目】已知圓C過點A(2,6),且與直線l1: x+y-10=0相切于點B(6,4).
(1)求圓C的方程;
(2)過點P(6,24)的直線l2與圓C交于M,N兩點,若△CMN為直角三角形,求直線l2的斜率;
(3)在直線l3: y=x-2上是否存在一點Q,過點Q向圓C引兩切線,切點為E,F, 使△QEF為正三角形,若存在,求出點Q的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產甲、乙兩種產品,已知生產每噸甲產品要用A原料3噸,B原料2噸;生產每噸乙產品要用A原料1噸,B原料3噸.銷售每噸甲產品可獲得利潤5萬元,每噸乙產品可獲得利潤3萬元.該企業在一個生產周期內消耗A原料不超過13噸,B原料不超過18噸.
(1)列出甲、乙兩種產品滿足的關系式,并畫出相應的平面區域;
(2)在一個生產周期內該企業生產甲、乙兩種產品各多少噸時可獲得利潤最大,最大利潤是多少?
(用線性規劃求解要畫出規范的圖形及具體的解答過程)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》是央視推出的一檔以“賞中華詩詞,尋文化基因,品生活之美”為宗旨的大型文化類競賽節目,邀請全國各個年齡段、各個領域的詩詞愛好者共同參與詩詞知識比拼。“百人團”由一百多位來自全國各地的選手組成,成員上至古稀老人,下至垂髫小兒,人數按照年齡分組統計如下表:
分組(年齡) |
|
|
|
頻數(人) |
|
|
|
(1)用分層抽樣的方法從“百人團”中抽取![]() 人參加挑戰,求從這三個不同年齡組中分別抽取的挑戰者的人數;
人參加挑戰,求從這三個不同年齡組中分別抽取的挑戰者的人數;
(2)在(1)中抽出的![]() 人中,任選
人中,任選![]() 人參加一對一的對抗比賽,求這
人參加一對一的對抗比賽,求這![]() 人來自同一年齡組的概率。
人來自同一年齡組的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝1261年所著的《詳解九章算法》一書里出現了如圖所示的表,即楊輝三角,這是數學史上的一個偉大成就,在“楊輝三角”中,第![]() 行的所有數字之和為
行的所有數字之和為![]() ,若去除所有為1的項,依次構成數列2,3,3,4,6,4,5,10,10,5,…,則此數列的前15項和為( )
,若去除所有為1的項,依次構成數列2,3,3,4,6,4,5,10,10,5,…,則此數列的前15項和為( )
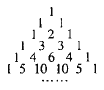
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長均相等的四棱錐![]() 中,
中, ![]() 為底面正方形的中心,
為底面正方形的中心, ![]() ,
,![]() 分別為側棱
分別為側棱![]() ,
,![]() 的中點,有下列結論正確的有:( )
的中點,有下列結論正確的有:( )
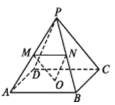
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直線![]() 與直線
與直線![]() 所成角的大小為
所成角的大小為![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正四棱錐![]() 中,O為頂點S在底面ABCD內的投影,P為側棱SD的中點,且
中,O為頂點S在底面ABCD內的投影,P為側棱SD的中點,且![]() .
.
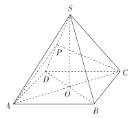
(1)證明:![]() 平面PAC.
平面PAC.
(2)求直線BC與平面PAC的所成角的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com