
【題目】在某單位的職工食堂中,食堂每天以![]() 元/個的價格從面包店購進面包,然后以
元/個的價格從面包店購進面包,然后以![]() 元/個的價格出售.如果當天賣不完,剩下的面包以
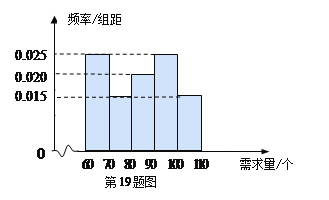
元/個的價格出售.如果當天賣不完,剩下的面包以![]() 元/個的價格賣給飼料加工廠.根據以往統計資料,得到食堂每天面包需求量的頻率分布直方圖如下圖所示.食堂某天購進了
元/個的價格賣給飼料加工廠.根據以往統計資料,得到食堂每天面包需求量的頻率分布直方圖如下圖所示.食堂某天購進了![]() 個面包,以
個面包,以![]() (單位:個,
(單位:個, ![]() )表示面包的需求量,
)表示面包的需求量, ![]() (單位:元)表示利潤.
(單位:元)表示利潤.
(Ⅰ)求![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(Ⅱ)求食堂每天面包需求量的中位數;
(Ⅲ)根據直方圖估計利潤![]() 不少于
不少于![]() 元的概率;
元的概率;
【答案】(Ⅰ) (Ⅱ)
(Ⅱ)![]() 個; (III)0.75
個; (III)0.75
【解析】試題分析:(1)當![]() 時,需求x,收入
時,需求x,收入![]() ,剩余90-x,虧損
,剩余90-x,虧損![]() ,總利潤T=
,總利潤T= ![]() -
-![]() =
=![]() ,當
,當![]() 時,面包全部賣出利潤
時,面包全部賣出利潤![]() ,寫成分段函數即求。(2)由頻率分布直方圖,[60,70]上P=0.25, [70,80]上P=0.15,[80,90]上P=0.2,0.25+0.15+0.2>0.5所以中位數在區間[80,90]上,設中位數為t
,寫成分段函數即求。(2)由頻率分布直方圖,[60,70]上P=0.25, [70,80]上P=0.15,[80,90]上P=0.2,0.25+0.15+0.2>0.5所以中位數在區間[80,90]上,設中位數為t![]() ,
,![]() ,可解得t。(3)由(Ⅰ)知,利潤
,可解得t。(3)由(Ⅰ)知,利潤![]() 不少于100元時,即
不少于100元時,即 ![]() ,
,![]() ,即
,即![]() ,
, ![]() =0.75
=0.75
試題解析:(Ⅰ)由題意,當![]() 時,利潤
時,利潤![]() ,
,
當![]() 時,利潤
時,利潤![]() ,
,
即
(Ⅱ)設食堂每天面包需求量的中位數為![]() ,則
,則
![]() ,解得
,解得![]() ,
,
故食堂每天面包需求量的中位數為![]() 個;
個;
(III)由題意,設利潤![]() 不少于100元為事件
不少于100元為事件![]() ,由(Ⅰ)知,利潤
,由(Ⅰ)知,利潤![]() 不少于100元時,
不少于100元時,
即 ![]() ,
,![]() ,即
,即![]() ,
,
由直方圖可知,當![]() 時,所求概率:
時,所求概率:
![]()


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ).
).
(1)當![]() 時,求函數
時,求函數![]() 的極值點;
的極值點;
(2)若函數![]() 在區間
在區間![]() 上恒有
上恒有![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)已知![]() ,且
,且![]() ,在(2)的條件下,證明數列
,在(2)的條件下,證明數列![]() 是單調遞增數列.
是單調遞增數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人每人有一張游泳比賽的門票,已知每張票可以觀看指定的三場比賽中的任一場(三場比賽時間不沖突),甲乙二人約定他們會觀看同一場比賽并且他倆觀看每場比賽的可能性相同,又已知丙觀看每一場比賽的可能性也相同,且甲乙的選擇與丙的選擇互不影響.
(1)求三人觀看同一場比賽的概率;
(2)記觀看第一場比賽的人數是![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x|x﹣a|
(1)若函數y=f(x)+x在R上是增函數,求實數a的取值范圍;
(2)若對任意x∈[1,2]時,函數f(x)的圖像恒在y=1圖像的下方,求實數a的取值范圍;
(3)設a≥2時,求f(x)在區間[2,4]內的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,已知點
中,已知點![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為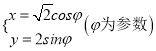 .以原點為極點,
.以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為 .
.
(Ⅰ)判斷點![]() 與直線
與直線![]() 的位置關系并說明理由;
的位置關系并說明理由;
(Ⅱ)設直線![]() 與曲線
與曲線![]() 的兩個交點分別為
的兩個交點分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() (
(![]() 為自然對數的底數).
為自然對數的底數).
(1)設曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,若
,若![]() 與點
與點![]() 的距離為
的距離為![]() ,求
,求![]() 的值;
的值;
(2)若對于任意實數![]() ,
, ![]() 恒成立,試確定
恒成立,試確定![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,函數
時,函數![]() 在
在![]() 上是否存在極值?若存在,請求出極值;若不存在,請說明理由.
上是否存在極值?若存在,請求出極值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+2x+c經過點A(0,3),B(﹣1,0),拋物線的頂點為點D,對稱軸與x軸交于點E,連結BD,則拋物線表達式:BD的長為 . 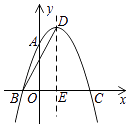
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x+2ax+b , 且f(1)= ![]() 、f(2)=
、f(2)= ![]() .
.
(1)求a、b的值;
(2)判斷f(x)的奇偶性并證明;
(3)先判斷并證明函數f(x)在[0,+∞)上的單調性,然后求f(x)的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com