
【題目】已知函數![]() (
(![]() 是自然對數的底數)
是自然對數的底數)
(1)求證: ![]()
(2)若不等式![]() 在
在![]() 上恒成立,求正數
上恒成立,求正數![]() 的取值范圍.
的取值范圍.
【答案】(1)見證明; (2) ![]()
【解析】
(1)要證ex≥x+1,只需證f(x)=ex﹣x﹣1≥0,求導得f′(x)=ex﹣1,利用導數性質能證明ex≥x+1.
(2)不等式f(x)>ax﹣1在x∈[![]() ,2]上恒成立,即a
,2]上恒成立,即a![]() 在x∈[
在x∈[![]() ]上恒成立,令g(x)
]上恒成立,令g(x)![]() ,x∈[
,x∈[![]() ],利用導數性質求g(x)
],利用導數性質求g(x)![]() 在x∈[
在x∈[![]() ]上的最小值,由此能求出正數a的取值范圍.
]上的最小值,由此能求出正數a的取值范圍.
(1)由題意知,要證![]() ,只需證
,只需證![]() ,
,
求導得![]() ,當
,當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
∴f(x)在![]() 是增函數,在
是增函數,在![]() 時是減函數,
時是減函數,
即![]() 在
在![]() 時取最小值
時取最小值![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
(2)不等式![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
亦即![]() 在x∈[
在x∈[![]() ,2]上恒成立,令g(x)=
,2]上恒成立,令g(x)=![]() ,
,![]() ,
,
以下求![]() 在
在![]() 上的最小值,
上的最小值,
![]() ,當
,當![]() 時,
時,![]() ,
,
當![]() ]時,
]時,![]() ,
,
∴當![]() ]時,
]時,![]() 單調遞減,當
單調遞減,當![]() ]時,
]時,![]() 單調遞增,
單調遞增,
∴![]() 在
在![]() 處取得最小值為
處取得最小值為![]() ,
,
∴正數a的取值范圍是![]() .
.


 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:高中數學 來源: 題型:
【題目】某超市隨機選取![]() 位顧客,記錄了他們購買甲、乙、丙、丁四種商品的情況,整理成如下統計表,其中“√”表示購買,“×”表示未購買.
位顧客,記錄了他們購買甲、乙、丙、丁四種商品的情況,整理成如下統計表,其中“√”表示購買,“×”表示未購買.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估計顧客同時購買乙和丙的概率;
(Ⅱ)估計顧客在甲、乙、丙、丁中同時購買![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顧客購買了甲,則該顧客同時購買乙、丙、丁中那種商品的可能性最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
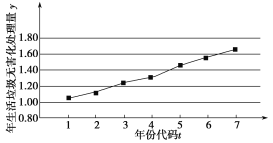
【題目】如圖是我國2012年至2018年生活垃圾無害化處理量(單位:億噸)的折線圖.注:年份代碼1~7分別對應年份2012~2018.
(1)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01),預測2020年我國生活垃圾無害化處理量.
的回歸方程(系數精確到0.01),預測2020年我國生活垃圾無害化處理量.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關系數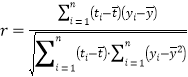 ,回歸方程
,回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為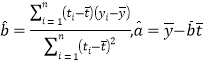 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了適應市場需求對產品結構做了重大調整,調整后初期利潤增長迅速,之后增長越來越慢,若要建立恰當的函數模型來反映該公司調整后利潤![]() 與時間
與時間![]() 的關系,可選用
的關系,可選用
A.一次函數B.二次函數
C.指數型函數D.對數型函數
查看答案和解析>>
科目:高中數學 來源: 題型:
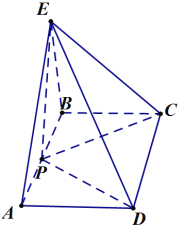
【題目】如圖,在矩形ABCD中,AB=2BC,P是線段AB中點,![]() 平面ABCD.
平面ABCD.
(1)求證:![]() 平面EPC;
平面EPC;
(2)問在EP上是否存在點F,使平面![]() 平面BFC?若存在,求出
平面BFC?若存在,求出![]() 的值;若不存在請說明理由.
的值;若不存在請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費用支出x(萬元)與銷售額y(萬元)之間有如下的對應數據:

(1)畫出散點圖;
(2)求回歸直線方程;
(3)據此估計廣告費用為9萬元時,銷售收入y的值.
注:①參考公式:線性回歸方程系數公式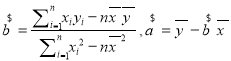 ;
;
②參考數據:![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com