
【題目】如圖1,在直角坐標系中,已知點A(0,2)、點B(-2,0),過點B和線段OA的中點C作直線BC,以線段BC為邊向上作正方形BCDE.
(1)填空:點D的坐標為_________,點E的坐標為_______________.
(2)若拋物線![]() 經(jīng)過A、D、E三點,求該拋物線的解析式.
經(jīng)過A、D、E三點,求該拋物線的解析式.
(3)若正方形和拋物線均以每秒![]() 個單位長度的速度沿射線BC同時向上平移,直至正方形的頂點E落在
個單位長度的速度沿射線BC同時向上平移,直至正方形的頂點E落在![]() 軸上時,正方形和拋物線均停止運動.
軸上時,正方形和拋物線均停止運動.
①在運動過程中,設(shè)正方形落在y軸右側(cè)部分的面積為![]() ,求
,求![]() 關(guān)于平移時間
關(guān)于平移時間![]() (秒)的函數(shù)關(guān)系式,并寫出相應(yīng)自變量
(秒)的函數(shù)關(guān)系式,并寫出相應(yīng)自變量![]() 的取值范圍.
的取值范圍.
②運動停止時,求拋物線的頂點坐標.
【答案】(1)D的坐標為(-1,3),E的坐標為(-3,2);
(2)拋物線的解析式為![]() ;
;
(3)①S與x的函數(shù)關(guān)系式為:
當0<t≤![]() 時, S=5
時, S=5![]()
當![]() <t≤1時,S=5t
<t≤1時,S=5t![]()
當1<t≤![]() 時,S=-5t2+15t
時,S=-5t2+15t![]()
②拋物線的頂點坐標是(![]() ,
, ![]() ).
).
【解析】(1)D(-1,3)、E(-3,2)(2分)
(2)拋物線經(jīng)過(0,2)、(-1,3)、(-3,2),則
![]()
解得 ![]()
∴![]()
(3)①當點D運動到y軸上時,t=![]() .
.
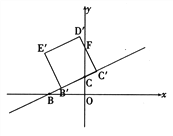
當0<t≤![]() 時,如右圖
時,如右圖
設(shè)D′C′交y軸于點F
∵tan∠BCO= ![]() =2,又∵∠BCO=∠FCC′
=2,又∵∠BCO=∠FCC′
∴tan∠FCC′=2, 即![]() =2
=2
∵CC′= ![]() t,∴FC′=2
t,∴FC′=2![]() t.
t.
∴S△CC′F =![]() CC′·FC′=
CC′·FC′= ![]() t×
t×![]() t=5 t2
t=5 t2
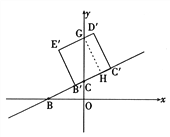 當點B運動到點C時,t=1.當
當點B運動到點C時,t=1.當![]() <t≤1時,如右圖
<t≤1時,如右圖
設(shè)D′E′交y軸于點G,過G作GH⊥B′C′于H.
在Rt△BOC中,BC= ![]()
∴GH= ![]() ,∴CH=
,∴CH=![]() GH=
GH= ![]()
∵CC′=![]() t,∴HC′=
t,∴HC′=![]() t-
t-![]() ,∴GD′=
,∴GD′=![]() t-
t-![]()
∴S梯形CC′D′G =![]() (
(![]() t-
t-![]() +
+ ![]() t)
t) ![]() =5t-
=5t-![]()
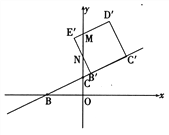 當點E運動到y軸上時,t=
當點E運動到y軸上時,t=![]() .
.
當1<t≤![]() 時,如右圖所示
時,如右圖所示
設(shè)D′E′、E′B′分別交y軸于點M、N
∵CC′=![]() t,B′C′=
t,B′C′=![]() ,
,
∴CB′=![]() t-
t-![]() ,∴B′N=2CB′=
,∴B′N=2CB′=![]() t-
t-![]()
∵B′E′=![]() ,∴E′N=B′E′-B′N=
,∴E′N=B′E′-B′N=![]() -
-![]() t
t
∴E′M=![]() E′N=
E′N=![]() (
(![]() -
-![]() t)
t)
∴S△MNE′ =![]() (
(![]() -
-![]() t)·
t)·![]() (
(![]() -
-![]() t)=5t2-15t+
t)=5t2-15t+![]()
∴S五邊形B′C′D′MN =S正方形B′C′D′E′ -S△MNE′ =![]() (5t2-15t+
(5t2-15t+![]() )=-5t2+15t-
)=-5t2+15t-![]()
綜上所述,S與x的函數(shù)關(guān)系式為:
當0<t≤![]() 時, S=5
時, S=5![]()
當![]() <t≤1時,S=5t
<t≤1時,S=5t![]()
當1<t≤![]() 時,S=-5t2+15t
時,S=-5t2+15t![]()
②當點E運動到點E′時,運動停止.如下圖所示
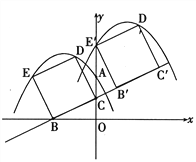 ∵∠CB′E′=∠BOC=90°,∠BCO=∠B′CE′
∵∠CB′E′=∠BOC=90°,∠BCO=∠B′CE′
∴△BOC∽△E′B′C
∴![]()
∵OB=2,B′E′=BC=![]()
∴![]()
∴CE′=![]()
∴OE′=OC+CE′=1+![]() =
=![]()
∴E′(0,![]() )
)
由點E(-3,2)運動到點E′(0, ![]() ),可知整條拋物線向右平移了3個單位,向上平移了
),可知整條拋物線向右平移了3個單位,向上平移了![]() 個單位.
個單位.
∵![]() =
= ![]()
∴原拋物線頂點坐標為(![]() ,
, ![]() )
)
∴運動停止時,拋物線的頂點坐標為(![]() ,
, ![]() )
)


科目:初中數(shù)學 來源: 題型:
【題目】“陽光體育”運動關(guān)乎每個學生未來的幸福生活,今年五月,我市某校開展了以“陽光體育我是冠軍”為主題的一分鐘限時跳繩比賽,要求每個班選2﹣3名選手參賽,現(xiàn)將80名選手比賽成績(單位:次/分鐘)進行統(tǒng)計.繪制成頻數(shù)分布直方圖,如圖所示.
(1)圖中a值為 .
(2)將跳繩次數(shù)在160~190的選手依次記為A1、A2、…An,從中隨機抽取兩名選手作經(jīng)驗交流,請用樹狀或列表法求恰好抽取到的選手A1和A2的概率.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,長方形AOBC在直角坐標系中,點A在y軸上,點B在x軸上,已知點C的坐標是(8,4).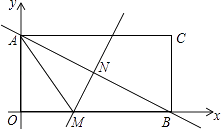
(1)求對角線AB所在直線的函數(shù)關(guān)系式;
(2)對角線AB的垂直平分線MN交x軸于點M,連接AM,求線段AM的長;
(3)若點P是直線AB上的一個動點,當△PAM的面積與長方形OABC的面積相等時,求點P的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
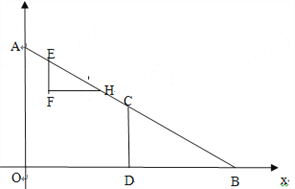
【題目】如圖,在直角坐標系中,點A(0,6),B(8,0),點C是線段AB的中點,CD⊥OB交OB于D,Rt△EFH的斜邊EH在射線AB上,頂點F在射線AB的左側(cè),EF∥OA,點E從點A出發(fā),以每秒1個單位的速度向B運動,到點B停止,AE=EF,運動時間為t(s).
(1)在Rt△EFH中,EF= ,EH= ,點F坐標為( , )(用含t的代數(shù)式表示)
(2)t為何值時,H與C重合?
(3)設(shè)△EFH與△CDB重疊部分圖形的面積為S(S>0),求S與t的函數(shù)關(guān)系式。
(4)在整個運動過程中,Rt△EFH掃過的面積是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列二次函數(shù)中,圖象以直線x=2為對稱軸、且經(jīng)過點(0,1)的是 ( )
A.y=(x-2)2+1B.y=(x+2)2+1
C.y=(x-2)2-3D.y=(x+2)2-3
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知多項式ax5+bx3+3x+c,當x=0時,該代數(shù)式的值為﹣1.
(1)求c的值;
(2)已知當x=3時,該式子的值為9,試求當x=﹣3時該式子的值;
(3)在第(2)小題的已知條件下,若有3a=5b成立,試比較a+b與c的大小?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com