
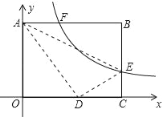
【題目】如圖,將矩形ABCO放在平面直角坐標系中,其中頂點B的坐標為(5,3),E是BC邊上一點,將△ABE沿AE翻折,點B剛好與OC邊上的點D重合,過點E的反比例函數y=![]() 的圖象與邊AB交于點F,則線段AF的長為_____.
的圖象與邊AB交于點F,則線段AF的長為_____.
【答案】![]()
【解析】
根據△ABE與△ADE是全等可得BE=DE,設BE=a=DE, CE=3-a,在Rt△AOD中,AD=AB=5,AO=3,由勾股定理![]() ,可得a的值,可求出反比例函數的表達式,可求出AF的長.
,可得a的值,可求出反比例函數的表達式,可求出AF的長.
解:根據題目條件可知, △ABE與△ADE是全等的,所以BE=DE,
設BE=a=DE, CE=3-a,
在Rt△AOD中,AD=AB=5,AO=3,由勾股定理![]() ,
,
即OD=![]() =4,
=4,
所以DC=OC-OD=1,
在Rt△DCE中, 由勾股定理![]() ,
,
即![]() ,求出a=
,求出a=![]() ,CE=
,CE=![]() ,
,
所以E(5,![]() ),
),
因為點E在反比例反函數上, 可得k =5![]()
![]() =
=![]() ,即可y=
,即可y=![]() ,
,
又因為點F在反比例函數上, 設F(b,3),
可得:b=![]() =
=![]() ,即AF的長為
,即AF的長為![]() .
.
故答案:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,AB=AC=10,線段BC在軸上,BC=12,點B的坐標為(﹣3,0),線段AB交y軸于點E,過A作AD⊥BC于D,動點P從原點出發,以每秒3個單位的速度沿x軸向右運動,設運動的時間為t秒.

(1)點E的坐標為( , );
(2)當△BPE是等腰三角形時,求t的值;
(3)若點P運動的同時,△ABC以B為位似中心向右放大,且點C向右運動的速度為每秒2個單位,△ABC放大的同時高AD也隨之放大,當以EP為直徑的圓與動線段AD所在直線相切,求t的值和此時C點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
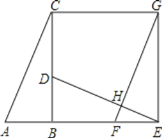
【題目】如圖,已知Rt△ABC中,∠ABC=90°,先把△ABC繞點B順時針旋轉90°至△DBE后,再把△ABC沿射線平移至△FEG,DF、FG相交于點H.
(1)判斷線段DE、FG的位置關系,并說明理由;
(2)連結CG,求證:四邊形CBEG是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐:
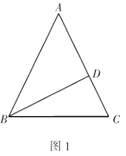
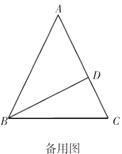
如圖1,![]() 中,
中,![]() ,
,![]() 于點
于點![]() ,
,![]() 且
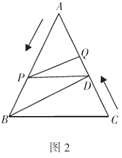
且![]() ;如圖2,在圖1的基礎上,動點
;如圖2,在圖1的基礎上,動點![]() 從點
從點![]() 出發以每秒
出發以每秒![]() 的速度沿線段
的速度沿線段![]() 向點
向點![]() 運動,同時動點
運動,同時動點![]() 從點
從點![]() 出發以相同速度沿線段
出發以相同速度沿線段![]() 向點
向點![]() 運動,當其中一點到達終點時另外一點也隨之停止運動,設點
運動,當其中一點到達終點時另外一點也隨之停止運動,設點![]() 運動的時間為
運動的時間為![]() 秒.
秒.
(1)求![]() 的長;
的長;
(2)當![]() 的其中一邊與
的其中一邊與![]() 平行時(
平行時(![]() 與
與![]() 不重合),求
不重合),求![]() 的值;
的值;
(3)點![]() 在線段
在線段![]() 上運動的過程中,是否存在以
上運動的過程中,是否存在以![]() 為腰的
為腰的![]() 是等腰三角形?若存在,求出
是等腰三角形?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每到春夏交替時節,雌性楊樹會以滿天飛絮的方式來傳播下一代,漫天飛舞的楊絮易引發皮膚病、呼吸道疾病等,給人們造成困擾,為了解市民對治理楊絮方法的贊同情況,某課題小組隨機調查了部分市民(問卷調查表如表所示),并根據調查結果繪制了如下尚不完整的統計圖.
治理楊絮一一您選哪一項?(單選)
A.減少楊樹新增面積,控制楊樹每年的栽種量
B.調整樹種結構,逐漸更換現有楊樹
C.選育無絮楊品種,并推廣種植
D.對雌性楊樹注射生物干擾素,避免產生飛絮
E.其他
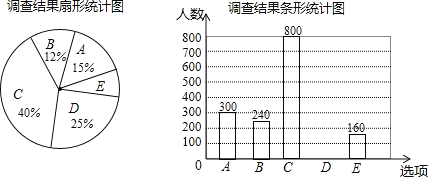
根據以上統計圖,解答下列問題:
(1)本次接受調查的市民共有 人;
(2)扇形統計圖中,扇形E的圓心角度數是 ;
(3)請補全條形統計圖;
(4)若該市約有90萬人,請估計贊同“選育無絮楊品種,并推廣種植”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】宜興在“創建文明城市”行動中,某社區計劃對面積為2160m2的區域進行綠化.經投標,由甲、乙兩個工程隊來完成,已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化面積的2倍,并且在獨立完成面積為480m2區域的綠化時,甲隊比乙隊少用4天.
(1)求甲、乙兩工程隊每天能完成綠化的面積;
(2)設甲工程隊施工x天,乙工程隊施工y天,剛好完成綠化任務,求y與x的函數表達式;
(3)若甲隊每天綠化費用是0.8萬元,乙隊每天綠化費用為0.35萬元,且甲、乙兩隊施工的總天數不超過26天,則如何安排甲乙兩隊施工的天數,使施工總費用最低?并求出最低費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是圓O的直徑,C、D是圓O上的點,且OC∥BD,AD分別與BC、OC相交于點E、F.則下列結論:
①AD⊥BD;②∠AOC=∠ABC;③CB平分∠ABD;④AF=DF;⑤BD=2OF.
其中一定成立的是( )

A.①③⑤ B.②③④ C.②④⑤ D.①③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
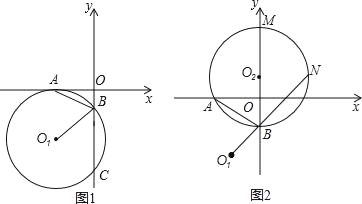
【題目】如圖1在平面直角坐標系中,⊙O1與x軸切于A(﹣3,0)與y軸交于B、C兩點,BC=8,連AB.
(1)求證:∠ABO1=∠ABO;
(2)求AB的長;
(3)如圖2,過A、B兩點作⊙O2與y軸的正半軸交于M,與O1B的延長線交于N,當⊙O2的大小變化時,得出下列兩個結論:①BM﹣BN的值不變;②BM+BN的值不變.其中有且只有一個結論正確,請判斷正確結論并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形![]() ,
,![]() ,
,![]() 與
與![]() 互補,以點
互補,以點![]() 為頂點作一個角,角的兩邊分別交線段
為頂點作一個角,角的兩邊分別交線段![]() ,
,![]() 于點
于點![]() ,
,![]() ,且
,且![]() ,連接
,連接![]() ,試探究:線段
,試探究:線段![]() ,
,![]() ,
,![]() 之間的數量關系.
之間的數量關系.
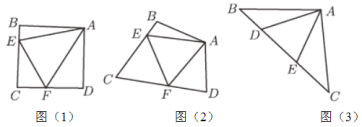
(1)如圖(1),當![]() 時,
時,![]() ,
,![]() ,
,![]() 之間的數量關系為___________.
之間的數量關系為___________.
(2)在圖(2)的條件下(即不存在![]() ),線段
),線段![]() ,
,![]() ,
,![]() 之間的數量關系是否仍然成立?若成立,請完成證明;若不成立,請說明理由.
之間的數量關系是否仍然成立?若成立,請完成證明;若不成立,請說明理由.
(3)如圖(3),在腰長為![]() 的等腰直角三角形
的等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 均在邊
均在邊![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com