
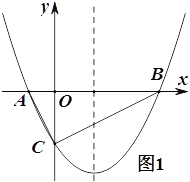
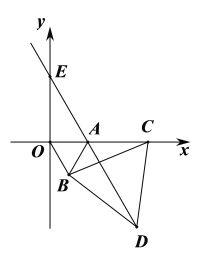
【題目】如圖,已知拋物線![]() (
(![]() >0)與
>0)與![]() 軸交于A,B兩點(A點在B點的左邊),與
軸交于A,B兩點(A點在B點的左邊),與![]() 軸交于點C。
軸交于點C。
(1)如圖1,若△ABC為直角三角形,求![]() 的值;
的值;
(2)如圖1,在(1)的條件下,點P在拋物線上,點Q在拋物線的對稱軸上,若以BC為邊,以點B,C,P,Q為頂點的四邊形是平行四邊形,求P點的坐標;
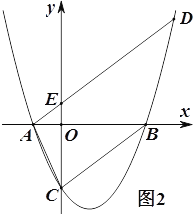
(3)如圖2,過點A作直線BC的平行線交拋物線于另一點D,交![]() 軸交于點E,若AE:ED=1:4,求
軸交于點E,若AE:ED=1:4,求![]() 的值.
的值.
【答案】(1)![]() ;(2)點P的坐標為
;(2)點P的坐標為![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用三角形相似可求AOOB,再由一元二次方程根與系數關系求AOOB構造方程求n;
(2)求出B、C坐標,設出點Q坐標,利用平行四邊形對角線互相平分性質,分類討論點P坐標,分別代入拋物線解析式,求出Q點坐標;
(3)設出點D坐標(a,b),利用相似表示OA,再由一元二次方程根與系數關系表示OB,得到點B坐標,進而找到b與a關系,代入拋物線求a、n即可.
(1)若△ABC為直角三角形
∴△AOC∽△COB
∴OC2=AOOB
當y=0時,0=![]() x2-
x2-![]() x-n
x-n
由一元二次方程根與系數關系
-OAOB=OC2
n2=![]() =2n
=2n
解得n=0(舍去)或n=2
∴拋物線解析式為y=![]() ;
;
(2)由(1)當![]() =0時
=0時
解得x1=-1,x2=4
∴OA=1,OB=4
∴B(4,0),C(0,-2)
∵拋物線對稱軸為直線x=-![]() =
=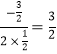
∴設點Q坐標為(![]() ,b)
,b)
由平行四邊形性質可知
當BQ、CP為平行四邊形對角線時,點P坐標為(![]() ,b+2)
,b+2)
代入y=![]() x2-
x2-![]() x-2
x-2
解得b=![]() ,則P點坐標為(
,則P點坐標為(![]() ,
,![]() )
)
當CQ、PB為為平行四邊形對角線時,點P坐標為(-![]() ,b-2)
,b-2)
代入y=![]() x2-
x2-![]() x-2
x-2
解得b=![]() ,則P坐標為(-
,則P坐標為(-![]() ,
,![]() )
)
綜上點P坐標為(![]() ,
,![]() ),(-
),(-![]() ,
,![]() );
);
(3)設點D坐標為(a,b)
∵AE:ED=1:4
則OE=![]() b,OA=
b,OA=![]() a
a
∵AD∥AB
∴△AEO∽△BCO
∵OC=n
∴![]()
∴OB=![]()
由一元二次方程根與系數關系得,![]()
∴b=![]() a2
a2
將點A(-![]() a,0),D(a,
a,0),D(a,![]() a2)代入y=
a2)代入y=![]() x2-
x2-![]() x-n
x-n
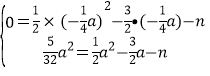
解得a=6或a=0(舍去)
則n=![]() .
.


 星級口算天天練系列答案
星級口算天天練系列答案科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,D是BC的中點,以AC為腰向外作等腰直角△ACE,∠EAC=90°,連接BE,交AD于點F,交AC于點G.
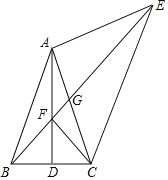
(1)若∠BAC=50°,求∠AEB的度數;
(2)求證:∠AEB=∠ACF;
(3)試判斷線段EF、BF與AC三者之間的等量關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
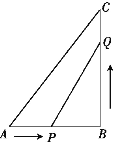
【題目】如圖,在△ABC中,∠B=90°,AB=5 cm,BC=7 cm,點P從點A開始沿AB邊向點B以1 cm/s的速度移動,同時點Q從點B開始沿BC向點C以2cm/s的速度移動.當一個點到達終點時另一點也隨之停止運動,運動時間為x秒(x>0).
(1)求幾秒后,PQ的長度等于5 cm.
(2)運動過程中,△PQB的面積能否等于8 cm2?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
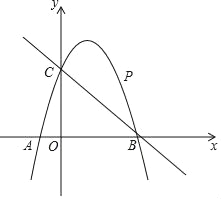
【題目】如圖,已知二次函數y=ax2+2x+c的圖象經過點C(0,3),與x軸分別交于點A,點B(3,0).點P是直線BC上方的拋物線上一動點.
(1)求二次函數y=ax2+2x+c的表達式;
(2)連接PO,PC,并把△POC沿y軸翻折,得到四邊形POP′C.若四邊形POP′C為菱形,請求出此時點P的坐標;
(3)當點P運動到什么位置時,四邊形ACPB的面積最大?求出此時P點的坐標和四邊形ACPB的最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
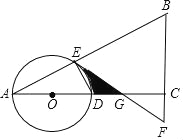
【題目】如圖,在△ABC中,∠ACB=90°,O是邊AC上一點,以O為圓心,以OA為半徑的圓分別交AB、AC于點E、D,在BC的延長線上取點F,使得BF=EF.
(1)判斷直線EF與⊙O的位置關系,并說明理由;
(2)若∠A=30°,求證:DG=![]() DA;
DA;
(3)若∠A=30°,且圖中陰影部分的面積等于2![]() ,求⊙O的半徑的長.
,求⊙O的半徑的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,以線段
,以線段![]() 為邊在第四象限內作等邊三角形
為邊在第四象限內作等邊三角形![]() ,點
,點![]() 為
為![]() 正半軸上一動點
正半軸上一動點![]() , 連接
, 連接![]() ,以線段
,以線段![]() 為邊在第四象限內作等邊三角形
為邊在第四象限內作等邊三角形![]() ,連接
,連接![]() 并延長,交
并延長,交![]() 軸于點
軸于點![]() .
.
(1)求證:![]() ≌
≌![]() ;
;
(2)在點![]() 的運動過程中,
的運動過程中,![]() 的度數是否會變化?如果不變,請求出
的度數是否會變化?如果不變,請求出![]() 的度數;如果變化,請說明理由.
的度數;如果變化,請說明理由.
(3)當點![]() 運動到什么位置時,以
運動到什么位置時,以![]() 為頂點的三角形是等腰三角形?
為頂點的三角形是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,點
,點![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與點
不與點![]() 重合),以
重合),以![]() 為腰作等腰直角
為腰作等腰直角![]() ,使
,使![]() ,連接
,連接![]() .
.
(1)觀察猜想
如圖1,當點![]() 在線段
在線段![]() 上時,
上時,
①![]() 與
與![]() 的位置關系為__________;
的位置關系為__________;
②![]() 之間的數量關系為___________(提示:可證
之間的數量關系為___________(提示:可證![]() )
)

(2)數學思考
如圖2,當點![]() 在線段
在線段![]() 的延長線上時,(1)中的①、②結論是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明;
的延長線上時,(1)中的①、②結論是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明;
(3)拓展延伸
如圖3,當點![]() 在線段
在線段![]() 的延長線時,將
的延長線時,將![]() 沿線段
沿線段![]() 翻折,使點
翻折,使點![]() 與點
與點![]() 重合,連接
重合,連接![]() ,若
,若![]() ,請直接寫出線段
,請直接寫出線段![]() 的長.(提示:做
的長.(提示:做![]() 于
于![]() ,做
,做![]() 于
于![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為創建“書香校園”,購置了一批圖書,已知購買科普類圖書花費10000元,購買文學類圖書花費9000元,其中科普類圖書平均每本的價格比文學類圖書平均每本的價格貴5元,且購買科普類圖書的數量與購買文學類圖書的數量相等.求科普類圖書平均每本的價格.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com