
【題目】某賓館客房部有![]() 個(gè)房間供游客居住,當(dāng)每個(gè)房間的定價(jià)為每天
個(gè)房間供游客居住,當(dāng)每個(gè)房間的定價(jià)為每天![]() 元時(shí),所有房間剛好可以住滿(mǎn),根據(jù)經(jīng)驗(yàn)發(fā)現(xiàn),每個(gè)房間的定價(jià)每增加
元時(shí),所有房間剛好可以住滿(mǎn),根據(jù)經(jīng)驗(yàn)發(fā)現(xiàn),每個(gè)房間的定價(jià)每增加![]() 元,就會(huì)有
元,就會(huì)有![]() 個(gè)房間空閑,對(duì)有游客入住的房間,賓館需對(duì)每個(gè)房間支出每天
個(gè)房間空閑,對(duì)有游客入住的房間,賓館需對(duì)每個(gè)房間支出每天![]() 元的各種費(fèi)用.設(shè)每個(gè)房間的定價(jià)增加
元的各種費(fèi)用.設(shè)每個(gè)房間的定價(jià)增加![]() 元,每天的入住量為
元,每天的入住量為![]() 個(gè),客房部每天的利潤(rùn)為
個(gè),客房部每天的利潤(rùn)為![]() 元.
元.
![]() 求
求![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
![]() 求
求![]() 與
與![]() 的函數(shù)關(guān)系式,并求客房部每天的最大利潤(rùn)是多少?
的函數(shù)關(guān)系式,并求客房部每天的最大利潤(rùn)是多少?
![]() 當(dāng)
當(dāng)![]() 為何值時(shí),客房部每天的利潤(rùn)不低于
為何值時(shí),客房部每天的利潤(rùn)不低于![]() 元?
元?
【答案】(1)![]() ;(2)
;(2)![]() , 當(dāng)
, 當(dāng)![]() 時(shí),
時(shí),![]() 有最大值,且最大值是
有最大值,且最大值是![]() 元;(3) 當(dāng)
元;(3) 當(dāng)![]() 時(shí),每天的利潤(rùn)不低于
時(shí),每天的利潤(rùn)不低于![]() 元.
元.
【解析】
(1)每個(gè)房間的定價(jià)增加![]() 元,則每天的入住量為
元,則每天的入住量為![]() ;
;
(2)客房部每天的利潤(rùn)=每個(gè)房間的定價(jià)×入住的房間數(shù)-成本,據(jù)此列出函數(shù)表達(dá)式,再將表達(dá)式化為一般式求最值即可;
(3)令W=1400,求解一元二次方程的兩個(gè)根,則x的范圍在兩根之間(含兩根)時(shí),符合題意.
解:![]() 由題意得:
由題意得:![]() ;
;
(2)![]()
∵![]() ,
,
∴當(dāng)![]() 時(shí),
時(shí),![]() 有最大值,且最大值是
有最大值,且最大值是![]() 元
元
![]() 當(dāng)
當(dāng)![]() 時(shí),即
時(shí),即![]() ,
,
解得:![]() ,
,![]() ,
,
故當(dāng)![]() 時(shí),每天的利潤(rùn)不低于
時(shí),每天的利潤(rùn)不低于![]() 元.
元.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)南水北調(diào)中線(xiàn)工程的起點(diǎn)是丹江口水庫(kù),按照工程計(jì)劃,需對(duì)原水庫(kù)大壩進(jìn)行混凝土培厚加高,使壩高由原來(lái)的162米增加到176.6米,以抬高蓄水位,如圖是某一段壩體加高工程的截面示意圖,其中原壩體的高為BE,背水坡坡角∠BAE=68°,新壩體的高為DE,背水坡坡角∠DCE=60°.求工程完工后背水坡底端水平方向增加的寬度AC.(結(jié)果精確到0.1米,參考數(shù)據(jù):sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.5,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知關(guān)于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是一個(gè)大于
是一個(gè)大于![]() 而小于
而小于![]() 的整數(shù),且方程的兩個(gè)根都是有理數(shù),求
的整數(shù),且方程的兩個(gè)根都是有理數(shù),求![]() 的值和它的兩個(gè)根;
的值和它的兩個(gè)根;
(2)若方程![]() 有兩個(gè)不相等的實(shí)數(shù)根,試判斷另一個(gè)關(guān)于
有兩個(gè)不相等的實(shí)數(shù)根,試判斷另一個(gè)關(guān)于![]() 的方程
的方程![]() 的根的情況.
的根的情況.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
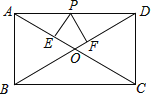
【題目】如圖所示,在矩形ABCD中,AB=6,AD=8,P是AD上的動(dòng)點(diǎn),PE⊥AC,PF⊥BD于F,則PE+PF的值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 、
、![]() 分別在邊
分別在邊![]() ,
,![]() 上,且
上,且![]() ,連接
,連接![]() ,將
,將![]() 對(duì)折,點(diǎn)
對(duì)折,點(diǎn)![]() 落在直線(xiàn)
落在直線(xiàn)![]() 上的點(diǎn)
上的點(diǎn)![]() 處,得折痕
處,得折痕![]() ;將
;將![]() 對(duì)折,點(diǎn)
對(duì)折,點(diǎn)![]() 落在直線(xiàn)
落在直線(xiàn)![]() 上的點(diǎn)
上的點(diǎn)![]() 處,得折痕
處,得折痕![]() ,當(dāng)
,當(dāng)![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上時(shí).若令
上時(shí).若令![]() 的面積為
的面積為![]() ,
,![]() 的長(zhǎng)度為
的長(zhǎng)度為![]() ,則
,則![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式是( )
的函數(shù)解析式是( )
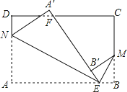
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸正半軸相交,其頂點(diǎn)坐標(biāo)為
軸正半軸相交,其頂點(diǎn)坐標(biāo)為![]() ,下列結(jié)論:①
,下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有兩個(gè)相等的實(shí)數(shù)根,其中正確的結(jié)論是________.(只填序號(hào)即可).
有兩個(gè)相等的實(shí)數(shù)根,其中正確的結(jié)論是________.(只填序號(hào)即可).
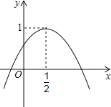
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在同一平面直角坐標(biāo)系中,一次函數(shù)y=kx﹣2k和二次函數(shù)y=﹣kx2+2x﹣4(k是常數(shù)且k≠0)的圖象可能是( )
A. 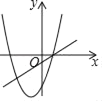 B.
B. 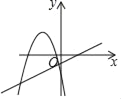
C. 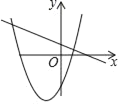 D.
D. 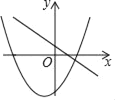
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】計(jì)算或解方程:
(1)計(jì)算下列各題
①(π﹣3.14)0+(﹣![]() )2﹣3﹣2;
)2﹣3﹣2;
②(3a﹣1)2﹣(3a﹣2)(3a+4);
③(12a5b7﹣8a4b6﹣4a4b2)÷(﹣2a2b)2;
(2)解分式方程:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,∠BAC=60°,∠BAC的平分線(xiàn)AD與邊BC的垂直平分線(xiàn)相交于點(diǎn)D,DE⊥AB交AB的延長(zhǎng)線(xiàn)于點(diǎn)E,DF⊥AC于點(diǎn)F,現(xiàn)有下列結(jié)論:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正確的有( )

A.![]() 個(gè)B.
個(gè)B.![]() 個(gè)C.
個(gè)C.![]() 個(gè)D.
個(gè)D.![]() 個(gè)
個(gè)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com