
【題目】如圖,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸正半軸相交,其頂點坐標(biāo)為
軸正半軸相交,其頂點坐標(biāo)為![]() ,下列結(jié)論:①
,下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有兩個相等的實數(shù)根,其中正確的結(jié)論是________.(只填序號即可).
有兩個相等的實數(shù)根,其中正確的結(jié)論是________.(只填序號即可).
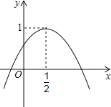
【答案】③④
【解析】
①根據(jù)拋物線的開口方向、對稱軸位置和拋物線與y軸的交點坐標(biāo)即可確定;
②根據(jù)拋物線的對稱軸即可判定;
③根據(jù)拋物線的頂點坐標(biāo)及b=-a即可判定;
④根據(jù)拋物線的最大值為1及二次函數(shù)與一元二次方程的關(guān)系即可判定.
①∵根據(jù)圖示知,拋物線開口方向向下,
∴a<0.
由對稱軸在y軸的右側(cè)知b>0,
∵拋物線與y軸正半軸相交,
∴c>0,
∴abc<0.故①錯誤;
②∵拋物線的對稱軸直線x=-![]() ,
,
∴a=-b.
故②錯誤;
③∵該拋物線的頂點坐標(biāo)為(![]() ,1),
,1),
∴1=![]() ,
,
∴b2-4ac=-4a.
∵b=-a,
∴a2-4ac=-4a,
∵a≠0,等式兩邊除以a,
得a-4c=-4,即a=4c-4.
故③正確;
④∵二次函數(shù)y=ax2+bx+c的最大值為1,即ax2+bx+c≤1,
∴方程ax2+bx+c=1有兩個相等的實數(shù)根.
故④正確.
綜上所述,正確的結(jié)論有③④.
故答案為:③④.


科目:初中數(shù)學(xué) 來源: 題型:
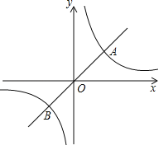
【題目】如圖,定義:若雙曲線![]() (k>0)與它的其中一條對稱軸y=x相交于A、B兩點,則線段AB的長度為雙曲線
(k>0)與它的其中一條對稱軸y=x相交于A、B兩點,則線段AB的長度為雙曲線![]() (k>0)的對徑.
(k>0)的對徑.
(1)求雙曲線![]() 的對徑.
的對徑.
(2)若雙曲線![]() (k>0)的對徑是
(k>0)的對徑是![]() ,求k的值.
,求k的值.
(3)仿照上述定義,定義雙曲線![]() (k<0)的對徑.
(k<0)的對徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 為
為![]() 的高,
的高,![]() 為
為![]() 角平分線,若
角平分線,若![]() .
.
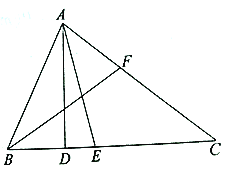
(1)求![]() 的度數(shù);
的度數(shù);
(2)求![]() 的度數(shù);
的度數(shù);
(3)若點![]() 為線段
為線段![]() 上任意一點,當(dāng)
上任意一點,當(dāng)![]() 為直角三角形時,則求
為直角三角形時,則求![]() 的度數(shù).
的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某賓館客房部有![]() 個房間供游客居住,當(dāng)每個房間的定價為每天
個房間供游客居住,當(dāng)每個房間的定價為每天![]() 元時,所有房間剛好可以住滿,根據(jù)經(jīng)驗發(fā)現(xiàn),每個房間的定價每增加
元時,所有房間剛好可以住滿,根據(jù)經(jīng)驗發(fā)現(xiàn),每個房間的定價每增加![]() 元,就會有
元,就會有![]() 個房間空閑,對有游客入住的房間,賓館需對每個房間支出每天
個房間空閑,對有游客入住的房間,賓館需對每個房間支出每天![]() 元的各種費用.設(shè)每個房間的定價增加
元的各種費用.設(shè)每個房間的定價增加![]() 元,每天的入住量為
元,每天的入住量為![]() 個,客房部每天的利潤為
個,客房部每天的利潤為![]() 元.
元.
![]() 求
求![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
![]() 求
求![]() 與
與![]() 的函數(shù)關(guān)系式,并求客房部每天的最大利潤是多少?
的函數(shù)關(guān)系式,并求客房部每天的最大利潤是多少?
![]() 當(dāng)
當(dāng)![]() 為何值時,客房部每天的利潤不低于
為何值時,客房部每天的利潤不低于![]() 元?
元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中(如圖),已知拋物線
中(如圖),已知拋物線![]() 經(jīng)過
經(jīng)過![]() ,
,![]() ,頂點為
,頂點為![]() .
.
![]() 求該拋物線的表達(dá)方式及點
求該拋物線的表達(dá)方式及點![]() 的坐標(biāo);
的坐標(biāo);
![]() 將
將![]() 中求得的拋物線沿
中求得的拋物線沿![]() 軸向上平移
軸向上平移![]() 個單位,所得新拋物線與
個單位,所得新拋物線與![]() 軸的交點記為點
軸的交點記為點![]() .當(dāng)
.當(dāng)![]() 時等腰三角形時,求點
時等腰三角形時,求點![]() 的坐標(biāo);
的坐標(biāo);
![]() 若點
若點![]() 在
在![]() 中求得的拋物線的對稱軸上,聯(lián)結(jié)
中求得的拋物線的對稱軸上,聯(lián)結(jié)![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針轉(zhuǎn)
逆時針轉(zhuǎn)![]() 得到線段
得到線段![]() ,若點
,若點![]() 恰好落在
恰好落在![]() 中求得的拋物線上,求點
中求得的拋物線上,求點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 與坐標(biāo)軸分別交于
與坐標(biāo)軸分別交于![]() 、
、![]() 兩點,拋物線
兩點,拋物線![]() 過
過![]() 、
、![]() 兩點,點
兩點,點![]() 為線段
為線段![]() 上一動點,過點
上一動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,交拋物線于點
,交拋物線于點![]() .
.
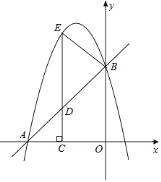
![]() 求拋物線的解析式.
求拋物線的解析式.
![]() 求
求![]() 面積的最大值.
面積的最大值.
![]() 連接
連接![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出點
相似?若存在,求出點![]() 坐標(biāo);若不存在,說明理由.
坐標(biāo);若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
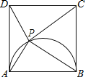
【題目】如圖,已知四邊形![]() 是邊長為
是邊長為![]() 的正方形,以
的正方形,以![]() 為直徑向正方形內(nèi)作半圓,
為直徑向正方形內(nèi)作半圓,![]() 為半圓上一動點(不與
為半圓上一動點(不與![]() 、
、![]() 重合),當(dāng)
重合),當(dāng)![]() ________時,
________時,![]() 為等腰三角形.
為等腰三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
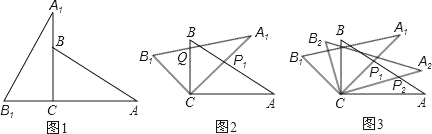
【題目】將兩塊全等的三角板如圖1擺放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)將圖1中△A1B1C繞點C順時針旋轉(zhuǎn)45°得圖2,點P1是A1C與AB的交點,點Q是A1B1與BC的交點,求證:CP1=CQ;
(2)在圖2中,若AP1=a,則CQ等于多少?
(3)將圖2中△A1B1C繞點C順時針旋轉(zhuǎn)到△A2B2C(如圖3),點P2是A2C與AP1的交點.當(dāng)旋轉(zhuǎn)角為多少度時,有△AP1C∽△CP1P2?這時線段CP1與P1P2之間存在一個怎樣的數(shù)量關(guān)系?.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com