
【題目】如圖,四棱錐![]() 中,
中, ![]() 為等邊三角形,且平面
為等邊三角形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)證明: ![]() ;
;
(Ⅱ)若棱錐![]() 的體積為
的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】【試題分析】(I) 取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
,![]() .利用等腰三角形的性質和矩形的性質可證得
.利用等腰三角形的性質和矩形的性質可證得![]() ,由此證得
,由此證得![]() 平面
平面![]() ,故
,故![]() ,故
,故![]() .(II) 可知
.(II) 可知![]() 是棱錐的高,利用體積公式求得
是棱錐的高,利用體積公式求得![]() ,利用勾股定理和等腰三角形的性質求得
,利用勾股定理和等腰三角形的性質求得![]() 的值,進而求得面積.
的值,進而求得面積.
【試題解析】
證明:(Ⅰ)取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
,![]() ,
,
∵![]() 為等邊三角形,∴
為等邊三角形,∴![]() .
.
底面![]() 中,可得四邊形
中,可得四邊形![]() 為矩形,∴
為矩形,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,所以
,所以![]() .
.
(Ⅱ)由面![]() 面
面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,所以
,所以![]() 為棱錐
為棱錐![]() 的高,
的高,
由![]() ,知
,知![]() ,
,
![]()
![]()
![]() ,
,
∴![]() .
.
由(Ⅰ)知![]() ,
,![]() ,∴
,∴![]() .
.
![]() .
.
由![]() ,可知
,可知![]() 平面
平面![]() ,∴
,∴![]() ,
,
因此![]() .
.
在![]() 中
中![]() ,
,![]() ,
,
取![]() 的中點
的中點![]() ,連結
,連結![]() ,則
,則![]() ,
,![]() ,
,
∴![]()
![]() .
.
所以棱錐![]() 的側面積為
的側面積為![]() .
.
【題型】解答題
【結束】
20
【題目】已知圓![]() 經過橢圓
經過橢圓![]() :
: ![]() 的兩個焦點和兩個頂點,點
的兩個焦點和兩個頂點,點![]() ,
, ![]() ,
, ![]() 是橢圓
是橢圓![]() 上的兩點,它們在
上的兩點,它們在![]() 軸兩側,且
軸兩側,且![]() 的平分線在
的平分線在![]() 軸上,
軸上, ![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)證明:直線![]() 過定點.
過定點.
【答案】(Ⅰ)![]() .(Ⅱ)直線
.(Ⅱ)直線![]() 過定點
過定點![]() .
.
【解析】【試題分析】(I)根據圓的半徑和已知 ![]() ,故
,故![]() ,由此求得橢圓方程.(II)設出直線
,由此求得橢圓方程.(II)設出直線![]() 的方程,聯立直線方程與橢圓方程,寫出韋達定理,寫出
的方程,聯立直線方程與橢圓方程,寫出韋達定理,寫出![]() 的斜率并相加,由此求得直線
的斜率并相加,由此求得直線![]() 過定點
過定點![]() .
.
【試題解析】
(Ⅰ)圓![]() 與
與![]() 軸交點
軸交點![]() 即為橢圓的焦點,圓
即為橢圓的焦點,圓![]() 與
與![]() 軸交點
軸交點![]() 即為橢圓的上下兩頂點,所以
即為橢圓的上下兩頂點,所以![]() ,
, ![]() .從而
.從而![]() ,
,
因此橢圓![]() 的方程為:
的方程為: ![]() .
.
(Ⅱ)設直線![]() 的方程為
的方程為![]() .
.
由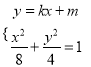 ,消去
,消去![]() 得
得![]() .
.
設![]() ,
, ![]() ,則
,則![]() ,
, ![]() .
.
直線![]() 的斜率
的斜率![]()
![]() ;
;
直線![]() 的斜率
的斜率![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
由![]() 的平分線在
的平分線在![]() 軸上,得
軸上,得![]() .又因為
.又因為![]() ,所以
,所以![]() ,
,
所以![]() .
.
因此,直線![]() 過定點
過定點![]() .
.
[點睛]本小題主要考查橢圓方程的求解,考查圓與橢圓的位置關系,考查直線與圓錐曲線位置關系. 涉及直線與橢圓的基本題型有:(1)位置關系的判斷.(2)弦長、弦中點問題.(3)軌跡問題.(4)定值、最值及參數范圍問題.(5)存在性問題.常用思想方法和技巧有:(1)設而不求.(2)坐標法.(3)根與系數關系.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:高中數學 來源: 題型:
【題目】一同學在電腦中打出若干個圈:○●○○●○○○●○○○○●○○○○○●…若將此若干個圈依此規律繼續下去,得到一系列的圈,那么在前2012個圈中的●的個數是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年6月14日,第二十一屆世界杯足球賽將在俄羅斯拉開帷幕.為了了解喜愛足球運動是否與性別有關,某體育臺隨機抽取100名觀眾進行統計,得到如下![]() 列聯表.
列聯表.

(1)將![]() 列聯表補充完整,并判斷能否在犯錯誤的概率不超過0.001的前提下認為喜愛足球運動與性別有關?
列聯表補充完整,并判斷能否在犯錯誤的概率不超過0.001的前提下認為喜愛足球運動與性別有關?
(2)在不喜愛足球運動的觀眾中,按性別分別用分層抽樣的方式抽取6人,再從這6人中隨機抽取2人參加一臺訪談節目,求這2人至少有一位男性的概率.
![]()

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD內接于⊙O,過點A作⊙O的切錢EP交CB 的延長線于P,己知∠PAB=25°. 
(1)若BC是⊙O的直徑,求∠D的大小;
(2)若∠DAE=25°,求證:DA2=DCBP.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把三盆不同的蘭花和4盆不同的玫瑰花擺放在右圖圖案中的1,2,3,4,5,6,7所示的位置上,其中三盆蘭花不能放在一條直線上,則不同的擺放方法為( ) 
A.2680種
B.4320種
C.4920種
D.5140種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有甲乙兩個班級進行數學考試,按照大于等于85分為優秀,85分以下為非優秀統計成績后,得到如下的列聯表.
| 優秀 | 非優秀 | 總計 |
甲班 | 10 | ||
乙班 | 30 | ||
總計 | 105 |
已知在全部105人中隨機抽取1人為優秀的概率為![]() .
.
(1)請完成上面的列聯表;(把列聯表自己畫到答題卡上)
(2)根據列聯表的數據,若按95%的可靠性要求,能否認為“成績與班級有關系”?
參考公式:![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用紅、黃、藍、白、黑五種顏色涂在如圖所示的四個區域內,每個區域涂一種顏色,相鄰兩個區域涂不同的顏色,五種顏色可以反復使用,共有___________種不同的涂色方法?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=x2﹣a|x﹣1|+b(a>0,b>﹣1)
(1)若b=0,a>2,求f(x)在區間[0,2]內的最小值m(a);
(2)若f(x)在區間[0,2]內不同的零點恰有兩個,且落在區間[0,1),(1,2]內各一個,求a﹣b的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com