
【題目】給出下列![]() 個結論:
個結論:
①棱長均相等的棱錐一定不是六棱錐;
②函數![]() 既不是奇函數又不是偶函數;
既不是奇函數又不是偶函數;
③若函數![]() 的值域為
的值域為![]() ,則實數
,則實數![]() 的取值范圍是
的取值范圍是![]() ;
;
④若函數![]() 滿足條件
滿足條件![]() ,則
,則![]() 的最小值為
的最小值為![]() .
.
其中正確的結論的序號是:______. (寫出所有正確結論的序號)
【答案】①,③,④
【解析】
對所給的四個結論分別進行分析、判斷后可得正確的結論的序號.
對于①,由平面幾何知識可得,正六邊形的中心到各頂點的距離等于邊長,此時中心與各頂點構成平面圖形,所以棱長均相等的棱錐一定不是六棱錐.所以①正確.
對于②,由![]() 得
得![]() ,故函數的定義域為
,故函數的定義域為![]() ,所以
,所以![]() ,所以
,所以![]() ,為偶函數.所以②不正確.
,為偶函數.所以②不正確.
對于③,設![]() ,由于函數的值域為
,由于函數的值域為![]() ,所以
,所以![]() 能夠取盡所有的正數,即函數
能夠取盡所有的正數,即函數![]() 的圖象與x軸有公共點.當
的圖象與x軸有公共點.當![]() 時,
時,![]() ,滿足題意;當
,滿足題意;當![]() 時,則有
時,則有![]() ,解得
,解得![]() .綜上可得實數
.綜上可得實數![]() 的取值范圍是
的取值范圍是![]() ,所以③正確.
,所以③正確.
對于④,以![]() 代替
代替![]() 中的
中的![]() 可得
可得![]() ,由
,由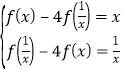 消去
消去![]() 整理得
整理得![]() ,所以
,所以![]() ,當且僅當
,當且僅當![]() ,即
,即![]() 時等號成立.所以④正確.
時等號成立.所以④正確.
綜上可得正確結論的序號為①③④.
故答案為①③④.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 中點.
中點.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 的動直線
的動直線![]() 與橢圓相交于
與橢圓相交于![]() 兩點,當直線
兩點,當直線![]() 與
與![]() 軸平行時,直線
軸平行時,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)在![]() 軸上是否存在異于點
軸上是否存在異于點![]() 的定點
的定點![]() ,使得直線
,使得直線![]() 變化時,總有
變化時,總有![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】統計表明,家庭的月理財投入![]() (單位:千元)與月收入
(單位:千元)與月收入![]() (單位:千元)之間具有線性相關關系.某銀行隨機抽取5個家庭,獲得第
(單位:千元)之間具有線性相關關系.某銀行隨機抽取5個家庭,獲得第![]() (
(![]() )個家庭的月理財投入
)個家庭的月理財投入![]() 與月收入
與月收入![]() 的數據資料,經計算得
的數據資料,經計算得![]() .
.
(1)求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() ;
;
(2)判斷![]() 與
與![]() 之間是正相關還是負相關;
之間是正相關還是負相關;
(3)若某家庭月理財投入為5千元,預測該家庭的月收入.
附:回歸方程的斜率與截距的最小二乘估計公式分別為:
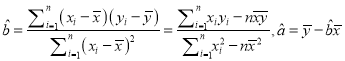 ,其中
,其中![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的右焦點F作漸近線的垂線,設垂足為P(P為第一象限的點),延長FP交拋物線y2=2px(p>0)于點Q,其中該雙曲線與拋物線有一個共同的焦點,若
=1(a>0,b>0)的右焦點F作漸近線的垂線,設垂足為P(P為第一象限的點),延長FP交拋物線y2=2px(p>0)于點Q,其中該雙曲線與拋物線有一個共同的焦點,若 ![]() =
= ![]() (
( ![]() +
+ ![]() ),則雙曲線的離心率的平方為( )
),則雙曲線的離心率的平方為( )
A.![]()
B.![]()
C.![]()
+1
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1 , F2分別為橢圓C: ![]() +
+ ![]() =1(a>b>0)的左、右兩個焦點,橢圓上點M(
=1(a>b>0)的左、右兩個焦點,橢圓上點M( ![]() ,
, ![]() )到F1、F2兩點的距離之和等于4.
)到F1、F2兩點的距離之和等于4.
(1)求橢圓C的方程;
(2)已知過右焦點且垂直于x軸的直線與橢圓交于點N(點N在第一象限),E,F是橢圓C上的兩個動點,如果kEN+KFN=0,證明直線EF的斜率為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產甲、乙兩種產品,已知生產每噸甲產品要用A原料3噸,B原料2噸,生產每噸乙產品要用A原料1噸,B原料3噸。銷售每噸甲產品可獲得利潤5萬元,每噸乙產品可獲得利潤3萬元,該企業在一個生產周期內消耗A原料不超過13噸,B原料不超過18噸,那么該企業可獲得最大利潤是___________萬元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com