
【題目】如果函數y=f(x)的導函數的圖象如圖所示,給出下列判斷:
①函數y=f(x)在區間 ![]() 內單調遞增;
內單調遞增;
②函數y=f(x)在區間 ![]() 內單調遞減;
內單調遞減;
③函數y=f(x)在區間(4,5)內單調遞增;
④當x=2時,函數y=f(x)有極小值;
⑤當x= ![]() 時,函數y=f(x)有極大值.
時,函數y=f(x)有極大值.
則上述判斷中正確的是( )
A.①②
B.②③
C.③④⑤
D.③
【答案】D
【解析】對于①,函數y=f(x)在區間(﹣3,﹣ ![]() )內有增有減,故①不正確;
)內有增有減,故①不正確;
對于②,函數y=f(x)在區間(﹣ ![]() ,3)有增有減,故②不正確;
,3)有增有減,故②不正確;
對于③,函數y=f(x)當x∈(4,5)時,恒有f′(x)>0.故③正確;
對于④,當x=2時,函數y=f(x)有極大值,故④不正確;
對于⑤,當x=﹣ ![]() 時,f′(x)≠0,故⑤不正確.
時,f′(x)≠0,故⑤不正確.
故答案為:D.
利用使f′(x)>0的區間是增區間,使f′(x)<0的區間是減區間,分別對①②③進行逐一判定,導數等于零的值是極值,先增后減是極大值,先減后增是極小值,再對④⑤進行判定.導數和函數的單調性的關系:
(1)若f′(x)>0在(a,b)上恒成立,則f(x)在(a,b)上是增函數,f′(x)>0的解集與定義域的交集的對應區間為增區間;
(2)若f′(x)<0在(a,b)上恒成立,則f(x)在(a,b)上是減函數,f′(x)<0的解集與定義域的交集的對應區間為減區間.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx,g(x)= ![]() ﹣
﹣ ![]() (x為實常數).
(x為實常數).
(1)當a=1時,求函數φ(x)=f(x)﹣g(x)在x∈[4,+∞)上的最小值;
(2)若方程e2f(x)=g(x)(其中e=2.71828…)在區間[ ![]() ]上有解,求實數a的取值范圍.
]上有解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知點G是△ABO的重心. 
(1)求 ![]() +
+ ![]() +
+ ![]() ;
;
(2)若PQ過△ABO的重心G,且 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =m
=m ![]() ,
, ![]() =n
=n ![]() ,求證:
,求證: ![]() +
+ ![]() =3.
=3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() x2-mln x,g(x)=x2-(m+1)x.
x2-mln x,g(x)=x2-(m+1)x.
(1)求函數f(x)的單調區間;
(2)當m≥0時,討論函數f(x)與g(x)圖象的交點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
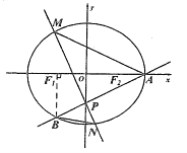
【題目】如圖,橢圓 ![]() 的右頂點為
的右頂點為 ![]() ,左、右焦點分別為
,左、右焦點分別為 ![]() ,過點
,過點 ![]() 且斜率為
且斜率為 ![]() 的直線與
的直線與 ![]() 軸交于點
軸交于點 ![]() ,與橢圓交于另一個點
,與橢圓交于另一個點 ![]() ,且點
,且點 ![]() 在
在 ![]() 軸上的射影恰好為點
軸上的射影恰好為點 ![]() .
.
(1)求橢圓 ![]() 的標準方程;
的標準方程;
(2)過點 ![]() 的直線與橢圓交于
的直線與橢圓交于 ![]() 兩點(
兩點( ![]() 不與
不與 ![]() 重合),若
重合),若 ![]() ,求直線
,求直線 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在空間中, ![]() 是兩條不同的直線,
是兩條不同的直線, ![]() 是兩個不同的平面,則下列命題中的真命題是( )
是兩個不同的平面,則下列命題中的真命題是( )
A.若 ![]() ,
, ![]() ,則
,則 ![]()
B.若 ![]() ,
, ![]() ,
, ![]() ,則
,則 ![]()
C.若 ![]() ,
, ![]() ,則
,則 ![]()
D.若 ![]() ,
, ![]() 則
則 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com