
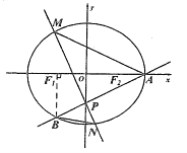
【題目】如圖,橢圓 ![]() 的右頂點為
的右頂點為 ![]() ,左、右焦點分別為
,左、右焦點分別為 ![]() ,過點
,過點 ![]() 且斜率為
且斜率為 ![]() 的直線與
的直線與 ![]() 軸交于點
軸交于點 ![]() ,與橢圓交于另一個點
,與橢圓交于另一個點 ![]() ,且點
,且點 ![]() 在
在 ![]() 軸上的射影恰好為點
軸上的射影恰好為點 ![]() .
.
(1)求橢圓 ![]() 的標準方程;
的標準方程;
(2)過點 ![]() 的直線與橢圓交于
的直線與橢圓交于 ![]() 兩點(
兩點( ![]() 不與
不與 ![]() 重合),若
重合),若 ![]() ,求直線
,求直線 ![]() 的方程.
的方程.
【答案】
(1)解:當 ![]() 時,
時, ![]() 軸,得到點
軸,得到點 ![]()
所以
![]()
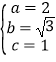 ,所以橢圓
,所以橢圓 ![]() 的方程是
的方程是 ![]()
(2)解:因為 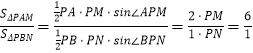 ,
, ![]() 所以
所以 ![]() .
.
設 ![]() ,則
,則 ![]() ,有
,有 ![]()
①當 ![]() 斜率不存在,
斜率不存在, ![]() 的方程為
的方程為 ![]() ,
,![]() 或
或 ![]() ,(不合條件,舍去)
,(不合條件,舍去)
②當 ![]() 斜率存在,由(Ⅰ)可知
斜率存在,由(Ⅰ)可知 ![]() ,設
,設 ![]() 方程為
方程為 ![]() ,
,
聯(lián)立方程 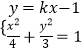 得:
得: ![]() .
.
由韋達定理可得 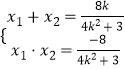 ,將
,將 ![]() 代入可得
代入可得 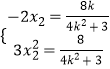 ,
,
即 ![]() .所以
.所以 ![]() .
.
所以直線 ![]() 的方程為
的方程為 ![]() 或
或 ![]()
【解析】(1)首先由條件得到直線AP的方程,根據(jù)“B和F1”的橫坐標相同可得到B的坐標,代入直線AP,得到a,b,c一組關系;再由橢圓的性質(zhì)a2=b2+c2得到一組關系;最后根據(jù)A點坐標,得到a=2,代入方程求解b,c的值。
(2)由上題已知A,B的坐標,面積之比為6,可以利用三角函數(shù)表示三角形的面積,將面積比轉(zhuǎn)化為邊長比,再轉(zhuǎn)化為向量比,向量由點的坐標表示,可設出M,N的坐標和直線MN的方程;聯(lián)立直線MN和橢圓,得到系數(shù)由k表示的一元二次方程,根據(jù)韋達定理得到x1和x2的關系,進而得到直線MN的斜率k。


 名牌中學課時作業(yè)系列答案
名牌中學課時作業(yè)系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,在矩形 ![]() 中,
中, ![]() 分別為
分別為 ![]() 的中點,現(xiàn)將
的中點,現(xiàn)將 ![]() 沿
沿 ![]() 折起,得四棱錐
折起,得四棱錐 ![]()
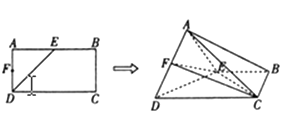
(1)求證: ![]() 平面
平面 ![]() ;
;
(2)若平面 ![]() 平面
平面 ![]() ,求四面體
,求四面體 ![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角△ABC中,∠BCA=90°,CA=CB=1,P為AB邊上的點且 ![]() =λ
=λ ![]() ,若
,若 ![]()
![]() ≥
≥ ![]()
![]() ,則λ的取值范圍是( )
,則λ的取值范圍是( )
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如果函數(shù)y=f(x)的導函數(shù)的圖象如圖所示,給出下列判斷:
①函數(shù)y=f(x)在區(qū)間 ![]() 內(nèi)單調(diào)遞增;
內(nèi)單調(diào)遞增;
②函數(shù)y=f(x)在區(qū)間 ![]() 內(nèi)單調(diào)遞減;
內(nèi)單調(diào)遞減;
③函數(shù)y=f(x)在區(qū)間(4,5)內(nèi)單調(diào)遞增;
④當x=2時,函數(shù)y=f(x)有極小值;
⑤當x= ![]() 時,函數(shù)y=f(x)有極大值.
時,函數(shù)y=f(x)有極大值.
則上述判斷中正確的是( )
A.①②
B.②③
C.③④⑤
D.③
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若關于x的不等式4ax-1<3x-4(a>0,且a≠1)對于任意的x>2恒成立,則a的取值范圍為( )
A.![]()
B.![]()
![]()
C.[2,+∞)
D.(2,+∞)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市初三畢業(yè)生參加中考要進行體育測試,某實驗中學初三(8)班的一次體育測試成績的莖葉圖和頻率分布直方圖都受到不同程度的涂黑,但可見部分如圖,據(jù)此解答如下問題.
(Ⅰ)求全班人數(shù)及中位數(shù),并重新畫出頻率直方圖;
(Ⅱ)若要從分數(shù)在 ![]() 之間的成績中任取兩個學生成績分析學生得分情況,在抽取的學生中,求至少有一個分數(shù)在
之間的成績中任取兩個學生成績分析學生得分情況,在抽取的學生中,求至少有一個分數(shù)在 ![]() 之間的概率.
之間的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù) ![]() .
.
(1)若曲線 ![]() 在
在 ![]() 處的切線經(jīng)過坐標原點,求
處的切線經(jīng)過坐標原點,求 ![]() 及該切線的方程;
及該切線的方程;
(2)設 ![]() ,若函數(shù)
,若函數(shù) ![]() 的值域為
的值域為 ![]() ,求實數(shù)
,求實數(shù) ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知y=f(x)是偶函數(shù),而y=f(x+1)是奇函數(shù),且對任意0≤x≤1,都有f(x)≥0,f(x)是增函數(shù),則a=f(2010),b=f( ![]() ),c=﹣f(
),c=﹣f( ![]() )的大小關系是( )
)的大小關系是( )
A.b<c<a
B.c<b<a
C.a<c<b
D.a<b<c
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com