【題目】設函數
（1）若函數
在
上遞增，在
上遞減，求實數
的值.
（2）討論
在
上的單調性；
（3）若方程
有兩個不等實數根
，求實數
的取值范圍，并證明
.
【答案】（1）
.（2）答案見解析.（3）
，證明見解析
【解析】
(1) 通過求導來判斷極值點，以此求出a的值;
（2）求導后對
分類討論，分
，
，
且
三種情況，討論函數的單調性即可；
（3）構造函數
，通過導數研究
的大致圖象，數形結合可得
的取值范圍，要證明
，即證
，即證
，做差轉化為利用導數研究函數
的最小值即可證明.
（1）由于函數
在
上遞增，在
上遞減，
由單調性知
是函數的極大值點，無極小值點，所以
，
∵
，
故
，
此時
滿足是極大值點，所以
；
（2）∵
，
∴
，
①當時，
在
上單調遞增.
②當，即
或
時，
，
∴
在上單調遞減.
③當且時，由
得
.
令
得
；
令得
.
∴在
上單調遞增，在
上單調遞減.
綜上，當時，在上遞增；
當或時，在上遞減；
當且時，在上遞增，在上遞減.
（3）令，
，
當
時，
，單調遞減；
當
時，
，單調遞增；
故
在
處取得最小值為
，
又當
，
所以函數大致圖象為：
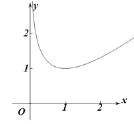
由圖象知：.
不妨設
，則有
，
要證，只需證
即可，
令，
則
在
上單調遞增，
故
即
，
，
.
智能訓練練測考系列答案科目：高中數學 來源： 題型：
【題目】將
顆珠子分成
堆.若通過每次從其中
堆中各取走一顆珠子，而最后取完，則稱這樣的分法為“和諧的”.試給出和諧分法的充分必要條件，并加以證明.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】凸多面體的每個面均為三角形，每條棱上均標記字母
之一，且每個面的三條邊上恰各有一個。對每一個面，當旋轉多面體使該面在我們眼前時，按照字母順序觀察其三邊，若是逆時針方向，則稱其為正面；否則，稱其為反面。證明：正面與反面的數目之差能被4整除。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知焦點在
軸上的拋物線
過點
，橢圓
的兩個焦點分別為
，其中
與的焦點重合，過
與長軸垂直的直線交橢圓于
兩點且
,曲線
是以原點為圓心以
為半徑的圓.
（1）求與及的方程；
（2）若動直線
與圓相切,且與交與
兩點,三角形
的面積為
，求的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4－4：坐標系與參數方程
在直角坐標系xOy中，曲線C1的普通方程為
，曲線C2參數方程為
為參數），以坐標原點O為極點，以x軸正半軸為極軸，建立極坐標系，直線l的極坐標方程為
．
（1）求C1的參數方程和
的直角坐標方程；
（2）已知P是C2上參數
對應的點，Q為C1上的點，求PQ中點M到直線的距離取得最大值時，點Q的直角坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將4個編號為1、2、3、4的小球放人編號為1、2、3、4的盒子中．
（1）恰好有一個空盒，有多少種放法？
（2）每個盒子放一個球，且恰好有一個球的編號與盒子的編號相同，有多少種放法？
（3）把4個不同的小球換成4個相同的小球，恰有一個空盒，有多少種放法？
查看答案和解析>>
科目：高中數學 來源： 題型：
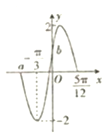
【題目】函數f（x）=Asin（2ωx+φ）（A＞0，ω＞0，|φ|＜
）的部分圖象如圖所示
（1）求A，ω，φ的值；
（2）求圖中a，b的值及函數f（x）的遞增區間；
（3）若α∈[0，π]，且f（α）=
，求α的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙二人獨立破譯同一密碼，甲破譯密碼的概率為
，乙破譯密碼的概率為
.記事件A：甲破譯密碼，事件B：乙破譯密碼.
（1）求甲、乙二人都破譯密碼的概率；
（2）求恰有一人破譯密碼的概率；
（3）小明同學解答“求密碼被破譯的概率”的過程如下：
解：“密碼被破譯”也就是“甲、乙二人中至少有一人破譯密碼”所以隨機事件“密碼被破譯”可以表示為
所以
請指出小明同學錯誤的原因？并給出正確解答過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
