
【題目】已知全集為實數集R,集合A={x|y= ![]() +
+ ![]() },B={x|log2x>1}.
},B={x|log2x>1}.
(1)分別求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求實數a的取值集合.
【答案】
(1)解:∵A={x|y= ![]() +
+ ![]() }={x|1≤x≤3},
}={x|1≤x≤3},
B={x|log2x>1}={x|x>2},
∴A∩B={x|2<x≤3},
∵CRB={x|x≤2},
∴(CRB)∪A={x|x≤2}∪{x|1≤x≤3}={x|x≤3}.
(2)解:①當a≤1時,C≠,此時CA;
②當a>1時,CA,則1<a≤3.
綜合①②,可得a的取值范圍是(﹣∞,3]
【解析】(1)由A={x|y= ![]() +
+ ![]() }={x|1≤x≤3},B={x|log2x>1}={x|x>2},能求出A∩B和(CRB)∪A.(2)當a≤1時,C≠,此時CA;當a>1時,CA,則1<a≤3,由此能求出a的取值范圍.
}={x|1≤x≤3},B={x|log2x>1}={x|x>2},能求出A∩B和(CRB)∪A.(2)當a≤1時,C≠,此時CA;當a>1時,CA,則1<a≤3,由此能求出a的取值范圍.
【考點精析】掌握交、并、補集的混合運算是解答本題的根本,需要知道求集合的并、交、補是集合間的基本運算,運算結果仍然還是集合,區分交集與并集的關鍵是“且”與“或”,在處理有關交集與并集的問題時,常常從這兩個字眼出發去揭示、挖掘題設條件,結合Venn圖或數軸進而用集合語言表達,增強數形結合的思想方法.


科目:高中數學 來源: 題型:
【題目】已知冪函數f(x)滿足:對任意x1 , x2∈R,當且僅當x1=x2時,有f(x1)=f(x2).則f(﹣1)+f(0)+f(1)的值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知y=f(x)是定義在R上的奇函數,且 ![]() 為偶函數,對于函數y=f(x)有下列幾種描述,其中描述正確的是( ) ①y=f(x)是周期函數;②x=π是它的一條對稱軸
為偶函數,對于函數y=f(x)有下列幾種描述,其中描述正確的是( ) ①y=f(x)是周期函數;②x=π是它的一條對稱軸
③(﹣π,0)是它圖象的一個對稱中心;④當 ![]() 時,它一定取最大值
時,它一定取最大值
A.①②
B.①③
C.②④
D.②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,AE:EB=1:2. 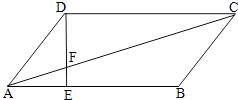
(1)求△AEF與△CDF的周長比;
(2)如果△AEF的面積等于6cm2 , 求△CDF的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列命題:
①命題:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x,則x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+![]() ,則x0∈(0,+∞),f(x0)=1;
,則x0∈(0,+∞),f(x0)=1;
④等差數列{an}的前n項和為Sn,若a4=3,則S7=21;
⑤在△ABC中,若A>B,則sinA>sinB.
其中真命題是____.(只填寫序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() ,將函數
,將函數 ![]() 的圖象按向量
的圖象按向量 ![]() 平移后得到函數g(x)的圖象.
平移后得到函數g(x)的圖象.
(1)求函數g(x)的表達式;
(2)若函數 ![]() 上的最小值為h(a),求h(a)的最大值.
上的最小值為h(a),求h(a)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的焦距為2,過短軸的一個端點與兩個焦點的圓的面積為
的焦距為2,過短軸的一個端點與兩個焦點的圓的面積為![]() ,過橢圓
,過橢圓![]() 的右焦點作斜率為
的右焦點作斜率為![]() (
(![]() )的直線
)的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 垂直于
垂直于![]() 的直線與
的直線與![]() 軸交于點
軸交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班有36名同學參加數學、物理、化學課外探究小組,每名同學至多參加兩個小組,已知參加數學、物理、化學小組的人數分別為26,15,13,同時參加數學和物理小組的有6人,同時參加物理和化學小組的有4人,則同時參加數學和化學小組的有人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com