
【題目】
已知函數(shù)![]() (
(![]() ),記
),記![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() .
.
(1)證明:當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
(2)若![]() 在
在![]() 處取得極小值,求
處取得極小值,求![]() 的取值范圍;
的取值范圍;
(3)設(shè)函數(shù)![]() 的定義域為
的定義域為![]() ,區(qū)間
,區(qū)間![]() ,若
,若![]() 在
在![]() 上是單調(diào)函數(shù),
上是單調(diào)函數(shù),
則稱![]() 在
在![]() 上廣義單調(diào).試證明函數(shù)
上廣義單調(diào).試證明函數(shù)![]() 在
在![]() 上廣義單調(diào).
上廣義單調(diào).
【答案】(1) 詳見解析;(2) ![]() ;(3) 詳見解析.
;(3) 詳見解析.
【解析】(1)試題分析:(1)當(dāng)![]() 時,
時,![]() ,
,
所以![]() ,即
,即![]() , 所以
, 所以![]() ,
,
所以![]() 在
在![]() 上單調(diào)遞增(2)因為
上單調(diào)遞增(2)因為![]() ,所以
,所以![]() .① 當(dāng)
.① 當(dāng)![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() ,
,
所以![]() 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是![]() ,單調(diào)減區(qū)間是
,單調(diào)減區(qū)間是![]() ,
,
所以![]() 在
在![]() 處取得極小值,符合題意. ② 當(dāng)
處取得極小值,符合題意. ② 當(dāng)![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞減.若
上單調(diào)遞減.若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() ,所以
,所以![]() 的單調(diào)減區(qū)間是
的單調(diào)減區(qū)間是![]() ,單調(diào)增區(qū)間是
,單調(diào)增區(qū)間是![]() ,所以
,所以![]() 在
在![]() 處取得極大值,不符合題意. ③ 當(dāng)
處取得極大值,不符合題意. ③ 當(dāng)![]() 時,
時,![]() ,使得
,使得![]() ,即
,即![]() ,但當(dāng)
,但當(dāng)![]() 時,
時,![]() ,即
,即![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞減,所以
上單調(diào)遞減,所以![]() ,即函數(shù)
,即函數(shù)![]() 在
在![]() 單調(diào)遞減,不符合題意.(3)記
單調(diào)遞減,不符合題意.(3)記![]() (
(![]() ),
),
① 若![]() ,注意到
,注意到![]() ,則
,則![]() ,即
,即![]() . 當(dāng)
. 當(dāng)![]() 時,
時,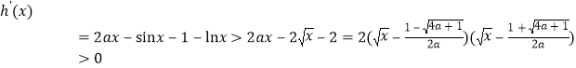 .所以
.所以![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
② 若![]() ,當(dāng)x>1時,
,當(dāng)x>1時,![]() <0.
<0.
所以![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
試題解析:
(1)當(dāng)![]() 時,
時,![]() ,
,
所以![]() ,即
,即![]() , 所以
, 所以![]() ,
,
所以![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
(2)因為![]() ,所以
,所以![]() .
.
① 當(dāng)![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() ,
,
所以![]() 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是![]() ,單調(diào)減區(qū)間是
,單調(diào)減區(qū)間是![]() ,
,
所以![]() 在
在![]() 處取得極小值,符合題意.
處取得極小值,符合題意.
② 當(dāng)![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞減.
上單調(diào)遞減.
若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() ,
,
所以![]() 的單調(diào)減區(qū)間是
的單調(diào)減區(qū)間是![]() ,單調(diào)增區(qū)間是
,單調(diào)增區(qū)間是![]() ,
,
所以![]() 在
在![]() 處取得極大值,不符合題意.
處取得極大值,不符合題意.
③ 當(dāng)![]() 時,
時,![]() ,使得
,使得![]() ,即
,即![]() ,
,
但當(dāng)![]() 時,
時,![]() ,即
,即![]() ,
,
所以函數(shù)![]() 在
在![]() 上單調(diào)遞減,所以
上單調(diào)遞減,所以![]() ,
,
即函數(shù)![]() 在
在![]() 單調(diào)遞減,不符合題意.
單調(diào)遞減,不符合題意.
綜上所述,![]() 的取值范圍是
的取值范圍是![]() .
.
(3)記![]() (
(![]() ),
),
① 若![]() ,注意到
,注意到![]() ,則
,則![]() ,即
,即![]() .
.
當(dāng)![]() 時,
時,![]()
![]() .
.
所以![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
② 若![]() ,當(dāng)x>1時,
,當(dāng)x>1時,![]() <0.
<0.
所以![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
綜上所述,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上廣義單調(diào).
上廣義單調(diào).


 小天才課時作業(yè)系列答案
小天才課時作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導(dǎo)學(xué)系列答案
新輔教導(dǎo)學(xué)系列答案 陽光同學(xué)一線名師全優(yōu)好卷系列答案
陽光同學(xué)一線名師全優(yōu)好卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】國內(nèi)某知名連鎖店分店開張營業(yè)期間,在固定的時間段內(nèi)消費達到一定標(biāo)準(zhǔn)的顧客可進行一次抽獎活動,隨著抽獎活動的有效展開,參與抽獎活動的人數(shù)越來越多,該分店經(jīng)理對開業(yè)前7天參加抽獎活動的人數(shù)進行統(tǒng)計,![]() 表示開業(yè)第
表示開業(yè)第![]() 天參加抽獎活動的人數(shù),得到統(tǒng)計表格如下:
天參加抽獎活動的人數(shù),得到統(tǒng)計表格如下:

經(jīng)過進一步的統(tǒng)計分析,發(fā)現(xiàn)![]() 與
與![]() 具有線性相關(guān)關(guān)系.
具有線性相關(guān)關(guān)系.
(1)根據(jù)上表給出的數(shù)據(jù),用最小二乘法,求出![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若該分店此次抽獎活動自開業(yè)始,持續(xù)10天,參加抽獎的每位顧客抽到一等獎(價值200元獎品)的概率為![]() ,抽到二等獎(價值100元獎品)的概率為
,抽到二等獎(價值100元獎品)的概率為![]() ,抽到三等獎(價值10元獎品)的概率為
,抽到三等獎(價值10元獎品)的概率為![]() ,試估計該分店在此次抽獎活動結(jié)束時送出多少元獎品?
,試估計該分店在此次抽獎活動結(jié)束時送出多少元獎品?
參考公式: ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以直角坐標(biāo)系的原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,并在兩種坐標(biāo)系中取相同的長度單位,已知直線
軸正半軸為極軸,并在兩種坐標(biāo)系中取相同的長度單位,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為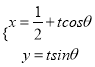 ,(
,( ![]() 為參數(shù),
為參數(shù), ![]() ),曲線
),曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,當(dāng)
兩點,當(dāng)![]() 變化時,求
變化時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在等邊△ABC中,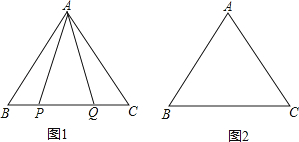
(1)如圖1,P,Q是BC邊上的兩點,AP=AQ,∠BAP=20°,求∠AQB的度數(shù);
(2)點P,Q是BC邊上的兩個動點(不與點B,C重合),點P在點Q的左側(cè),且AP=AQ,點Q關(guān)于直線AC的對稱點為M,連接AM,PM.
①依題意將圖2補全;
②小茹通過觀察、實驗提出猜想:在點P,Q運動的過程中,始終有PA=PM,小茹把這個猜想與同學(xué)們進行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:要證明PA=PM,只需證△APM是等邊三角形;
想法2:在BA上取一點N,使得BN=BP,要證明PA=PM,只需證△ANP≌△PCM;
想法3:將線段BP繞點B順時針旋轉(zhuǎn)60°,得到線段BK,要證PA=PM,只需證PA=CK,PM=CK…
請你參考上面的想法,幫助小茹證明PA=PM(一種方法即可).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高三文科500名學(xué)生參加了5月份的模擬考試,學(xué)校為了了解高三文科學(xué)生的數(shù)學(xué)、語文情況,利用隨機數(shù)表法從中抽取100名學(xué)生的成績進行統(tǒng)計分析,抽出的100名學(xué)生的數(shù)學(xué)、語文成績?nèi)缦卤恚?/span>

(1)將學(xué)生編號為:001,002,003,……,499,500.若從第5行第5列的數(shù)開始右讀,請你依次寫出最先抽出的5個人的編號(下面是摘自隨機數(shù)表的第4行至第7行)

(2)若數(shù)學(xué)的優(yōu)秀率為![]() ,求
,求![]() 的值;
的值;
(3)在語文成績?yōu)榱己玫膶W(xué)生中,已知![]() ,求數(shù)學(xué)成績“優(yōu)”比“良”的人數(shù)少的概率.
,求數(shù)學(xué)成績“優(yōu)”比“良”的人數(shù)少的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}的首項a1=a,其前n項和為Sn , 且滿足Sn+Sn﹣1=3n2+2n+4(n≥2),若對任意的n∈N* , an<an+1恒成立,則a的取值范圍是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列{an}是等差數(shù)列,前n項和為Sn , {bn}是單調(diào)遞增的等比數(shù)列,b1=2是a1與a2的等差中項,a3=5,b3=a4+1,若當(dāng)n≥m時,Sn≤bn恒成立,則m的最小值為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】要得到函數(shù)y=cos(2x+1)的圖象,只要將函數(shù)y=cos2x的圖象( )
A.向左平移1個單位
B.向右平移1個單位
C.向左平移 ![]() 個單位
個單位
D.向右平移 ![]() 個單位
個單位
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某食品廠為了檢查甲、乙兩條自動包裝流水線的生產(chǎn)情況,隨機在這兩條流水線上各抽取40件產(chǎn)品作為樣本,并稱出它們的重量(單位:克),重量值落在![]() 內(nèi)的產(chǎn)品為合格品,否則為不合格品,統(tǒng)計結(jié)果如表:
內(nèi)的產(chǎn)品為合格品,否則為不合格品,統(tǒng)計結(jié)果如表:
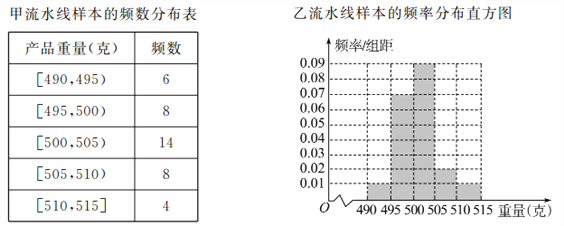
(Ⅰ)求甲流水線樣本合格的頻率;
(Ⅱ)從乙流水線上重量值落在![]() 內(nèi)的產(chǎn)品中任取2個產(chǎn)品,求這2件產(chǎn)品中恰好只有一件合格的概率.
內(nèi)的產(chǎn)品中任取2個產(chǎn)品,求這2件產(chǎn)品中恰好只有一件合格的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com