
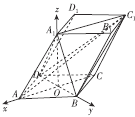
【題目】如圖所示,在底面為正方形的四棱柱![]() 中,
中, ![]() .
.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析(2)![]()
【解析】試題分析:
(1)連![]() 交
交![]() 于
于![]() ,由條件可得
,由條件可得![]() ,又由
,又由![]() 得到
得到 ![]() ,從而可得
,從而可得![]() 平面
平面![]() .由四邊形
.由四邊形![]() 為平行四邊形可得
為平行四邊形可得![]() ,所以
,所以![]() 平面
平面![]() ,因此平面
,因此平面![]() 平面
平面![]() .(2)由條件可得
.(2)由條件可得![]() 兩兩垂直,建立空間直角坐標系,求出平面
兩兩垂直,建立空間直角坐標系,求出平面![]() 的法向量和直線
的法向量和直線![]() 的法向量,根據兩向量的夾角的余弦值可求得線面角的正弦值.
的法向量,根據兩向量的夾角的余弦值可求得線面角的正弦值.
試題解析:
(1)證明:連![]() 交
交![]() 于
于![]() ,則
,則![]() 為
為![]() 中點,
中點,
∵![]() ,
,
∴![]() .
.
∵![]() ,
, ![]() 為公共邊,
為公共邊,
∴![]() ,
,
∴![]() .
.
又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() .
.
由題意得![]() ,故四邊形
,故四邊形![]() 為平行四邊形.
為平行四邊形.
∴![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() 內,
內,
∴ 平面![]() 平面
平面![]() .
.
(2)由題意得![]() 兩兩垂直,建立如圖所示的空間直角坐標系
兩兩垂直,建立如圖所示的空間直角坐標系![]() ,
,
∵![]() ,
,
∴![]() 為等邊三角形,
為等邊三角形,
∴![]() .
.
又![]() ,
,
∴![]() .
.
則![]() .
.
∴![]() ,
, ![]() ,
,
![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
由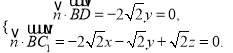 可得
可得![]() ,
,
令![]() ,則
,則 ![]() .
.
設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
則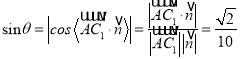 .
.
所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】據中國日報網報道:2017年11月13日,TOP500發布的最新一期全球超級計算機500強榜單顯示,中國超算在前五名中占據兩席.其中超算全球第一“神威·太湖之光”完全使用了國產品牌處理器.為了了解國產品牌處理器打開文件的速度,某調查公司對兩種國產品牌處理器進行了12次測試,結果如下:(數值越小,速度越快,單位是MIPS)

(Ⅰ)從品牌![]() 的12次測試中,隨機抽取一次,求測試結果小于7的概率;
的12次測試中,隨機抽取一次,求測試結果小于7的概率;
(Ⅱ)從12次測試中,隨機抽取三次,記![]() 為品牌
為品牌![]() 的測試結果大于品牌
的測試結果大于品牌![]() 的測試結果的次數,求
的測試結果的次數,求![]() 的分布列和數學期望
的分布列和數學期望![]() ;
;
(Ⅲ)經過了解,前6次測試是打開含有文字與表格的文件,后6次測試時打開含有文字與圖片的文件.請你依據表中數據,運用所學的統計知識,對這兩種國產品牌處理器打開文件的速度進行評價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() ,其中
,其中![]()
![]() .
. ![]() 表示
表示![]()
![]() 中所有不同值的個數.
中所有不同值的個數.
(Ⅰ)若集合![]() ,求
,求![]() ;
;
(Ⅱ)若集合![]() ,求證:
,求證: ![]() 的值兩兩不同,并求
的值兩兩不同,并求![]() ;
;
(Ⅲ)求![]() 的最小值.(用含
的最小值.(用含![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校初三年級有![]() 名學生,隨機抽查了
名學生,隨機抽查了![]() 名學生,測試
名學生,測試![]() 分鐘仰臥起坐的成績(次數),將數據整理后繪制成如圖所示的頻率分布直方圖.用樣本估計總體,下列結論正確的是( )
分鐘仰臥起坐的成績(次數),將數據整理后繪制成如圖所示的頻率分布直方圖.用樣本估計總體,下列結論正確的是( )

A. 該校初三年級學生![]() 分鐘仰臥起坐的次數的中位數為
分鐘仰臥起坐的次數的中位數為![]() 次
次
B. 該校初三年級學生![]() 分鐘仰臥起坐的次數的眾數為
分鐘仰臥起坐的次數的眾數為![]() 次
次
C. 該校初三年級學生![]() 分鐘仰臥起坐的次數超過
分鐘仰臥起坐的次數超過![]() 次的人數約有
次的人數約有![]() 人
人
D. 該校初三年級學生![]() 分鐘仰臥起坐的次數少于
分鐘仰臥起坐的次數少于![]() 次的人數約為
次的人數約為![]() 人.
人.
查看答案和解析>>
科目:高中數學 來源: 題型:
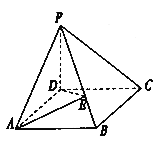
【題目】如圖在棱錐![]() 中,
中, ![]() 為矩形,
為矩形, ![]() 面
面![]() ,
, ![]() ,
, ![]() 與面
與面![]() 成
成![]() 角,
角, ![]() 與面
與面![]() 成
成![]() 角.
角.
(1)在![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 面
面![]() ,若存在確定
,若存在確定![]() 點位置,若不存在,請說明理由;
點位置,若不存在,請說明理由;
(2)當![]() 為
為![]() 中點時,求二面角
中點時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了準確把握市場,做好產品計劃,特對某產品做了市場調查:先銷售該產品50天,統計發現每天的銷售量![]() 分布在
分布在![]() 內,且銷售量
內,且銷售量![]() 的分布頻率
的分布頻率
 .
.
(Ⅰ)求![]() 的值并估計銷售量的平均數;
的值并估計銷售量的平均數;
(Ⅱ)若銷售量大于等于70,則稱該日暢銷,其余為滯銷.在暢銷日中用分層抽樣的方法隨機抽取8天,再從這8天中隨機抽取3天進行統計,設這3天來自![]() 個組,求隨機變量
個組,求隨機變量![]() 的分布列及數學期望(將頻率視為概率).
的分布列及數學期望(將頻率視為概率).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下面四個類比結論:
①實數a,b,若ab=0,則a=0或b=0;類比復數z1,z2,若z1z2=0,則z1=0或z2=0.
②實數a,b,若ab=0,則a=0或b=0;類比向量a,b,若a·b=0,則a=0或b=0.
③實數a,b,有a2+b2=0,則a=b=0;類比復數z1,z2,有z+z=0,則z1=z2=0.
④實數a,b,有a2+b2=0,則a=b=0;類比向量a,b,若a2+b2=0,則a=b=0.
其中類比結論正確的個數是( )
A. 0 B. 1
C. 2 D. 3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com