【題目】關于函數
，有下列命題：①當
時，
是增函數；當
時，是減函數；②其圖象關于
軸對稱；③無最大值，也無最小值；④在區間
上是增函數；⑤的最小值是
。其中所有不正確命題的序號是________
科目：高中數學 來源： 題型：
【題目】已知定義在實數集
上的偶函數
和奇函數
滿足
.
（1）求與的解析式；
（2）求證：在區間
上單調遞增；并求在區間的反函數；
（3）設
（其中
為常數），若
對于
恒成立，求的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列
滿足
，
，
，
.s
（1）證明：數列
是等差數列，并求數列的通項；
（2）求數列的通項，并求數列
的前
項和
；
（3）若
，且
是單調遞增數列，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，
為橢圓
的下頂點.過的直線
交拋物線
于
，
兩點，是
的中點.
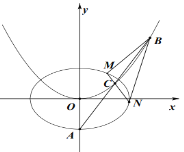
（1）求證：點的縱坐標是定值；
（2）過點作與直線傾斜角互補的直線
交橢圓于
，
兩點.求
的值，使得
的面積最大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）的定義域為（﹣∞，0）∪（0，+∞），f（x）是奇函數，且當x＞0時，f（x）=x2﹣x+a，若函數g（x）=f（x）﹣x的零點恰有兩個，則實數a的取值范圍是（ ）
A.a＜0B.a≤0C.a≤1D.a≤0或a=1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業有甲、乙兩條生產線生產同一種產品，為了檢測兩條生產線產品的質量情況，隨機從兩條生產線 生產的大量產品中各抽取了 40件產品作為樣本，檢測某一項質量指標值
，得到如圖所示的頻率分布直方圖，若
，亦則該產品為示合格產品，若
，則該產品為二等品，若
，則該產品為一等品.
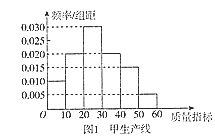
（1）用樣本估計總體的思想，從甲、乙兩條生產線中各隨機抽取一件產品，試估計這兩件產品中恰好一件為二等品，一件為一等品的概率；
（2）根據圖1和圖2，對兩條生產線從樣本的平均值和方差方面進行比較，哪一條生產線更好；
（3）從甲生產線的樣本中，滿足質量指標值在
的產品中隨機選出3件，記
為指標值在
中的件數，求的分布列和數學期望
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】公元263年左右，我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時，多邊形面積可無限逼近圓的面積，并創立了“割圓術”，利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14，這就是著名的“徽率”．如圖是利用劉徽的“割圓術”思想設計的一個程序框圖，則輸出n的值為（ ）（參考數據：sin15°=0.2588，sin7.5°=0.1305）
A. 12B. 24C. 48D. 96
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
